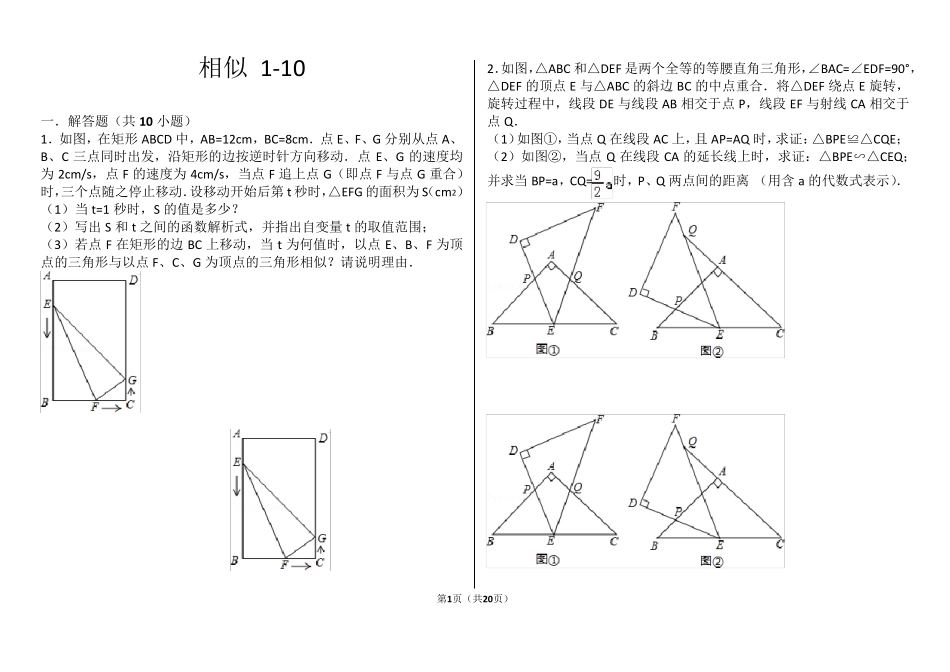
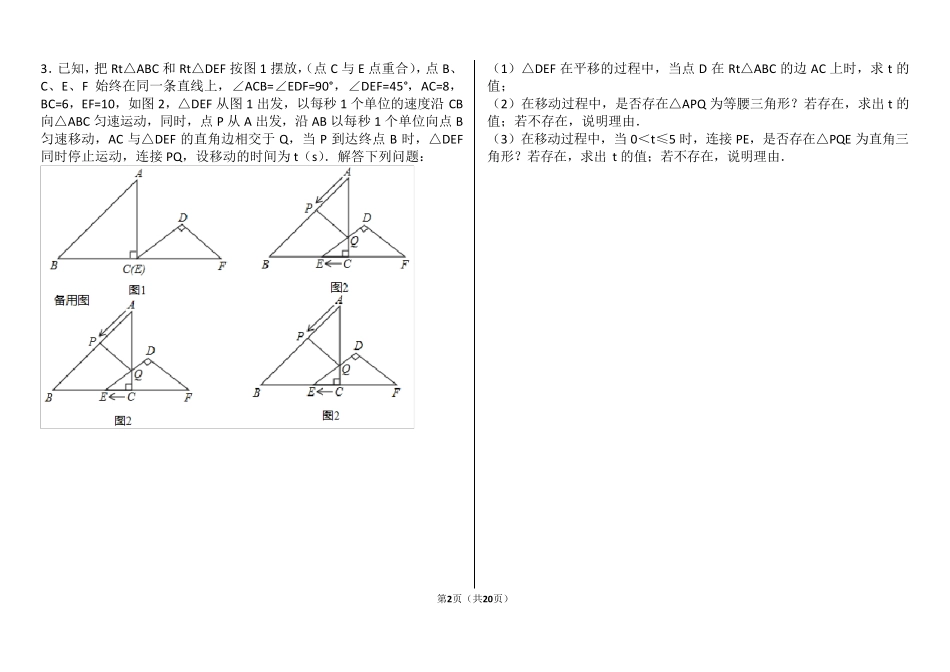
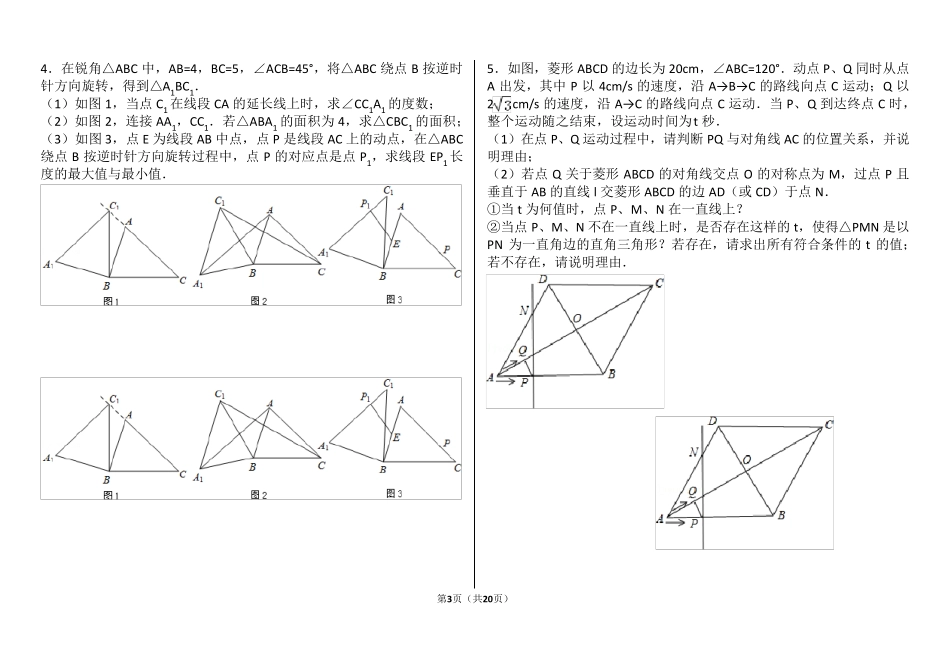
第1页(共20页) 相似 1-10 一.解答题(共10 小题) 1.如图,在矩形ABCD 中,AB=12cm,BC=8cm.点E、F、G 分别从点A、B、C 三点同时出发,沿矩形的边按逆时针方向移动.点E、G 的速度均为2cm/s,点F 的速度为4cm/s,当点F 追上点G(即点F 与点G 重合)时,三个点随之停止移动.设移动开始后第t 秒时,△EFG 的面积为S(cm2) (1)当t=1 秒时,S 的值是多少? (2)写出S 和t 之间的函数解析式,并指出自变量t 的取值范围; (3)若点F 在矩形的边BC 上移动,当t 为何值时,以点E、B、F 为顶点的三角形与以点F、C、G 为顶点的三角形相似?请说明理由. 2.如图,△ABC 和△DEF 是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF 的顶点E 与△ABC 的斜边BC 的中点重合.将△DEF 绕点E 旋转,旋转过程中,线段 DE 与线段 AB 相交于点P,线段 EF 与射线 CA 相交于点Q. (1)如图①,当点Q 在线段 AC 上,且 AP=AQ 时,求证:△BPE≌△CQE; (2)如图②,当点Q 在线段 CA 的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=时,P、Q 两点间的距离 (用含 a 的代数式表示). 第2页(共20页) 3.已知,把Rt△ABC 和Rt△DEF 按图1 摆放,(点C 与E 点重合),点B、C、E、F 始终在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8,BC=6,EF=10,如图2,△DEF 从图1 出发,以每秒 1 个单位的速度沿 CB向△ABC 匀速运动,同时,点P 从 A 出发,沿 AB 以每秒 1 个单位向点B匀速移动,AC 与△DEF 的直角边相交于 Q,当 P 到达终点B 时,△DEF同时停止运动,连接 PQ,设移动的时间为 t(s).解答下列问题: (1)△DEF 在平移的过程中,当点D 在Rt△ABC 的边 AC 上时,求 t 的值; (2)在移动过程中,是否存在△APQ 为等腰三角形?若存在,求出 t 的值;若不存在,说明理由. (3)在移动过程中,当 0<t≤5 时,连接 PE,是否存在△PQE 为直角三角形?若存在,求出 t 的值;若不存在,说明理由. 第3页(共20页) 4.在锐角△ABC 中,AB=4,BC=5,∠ACB=45°,将△ABC 绕点 B 按逆时针方向旋转,得到△A1BC1. (1)如图 1,当点 C1 在线段 CA 的延长线上时,求∠CC1A1 的度数; (2)如图 2,连接 AA1,CC1.若△ABA1 的面积为 4,求△CBC1 的面积; (3)如图 3,点 E 为线段 AB 中点,点 P 是线段...