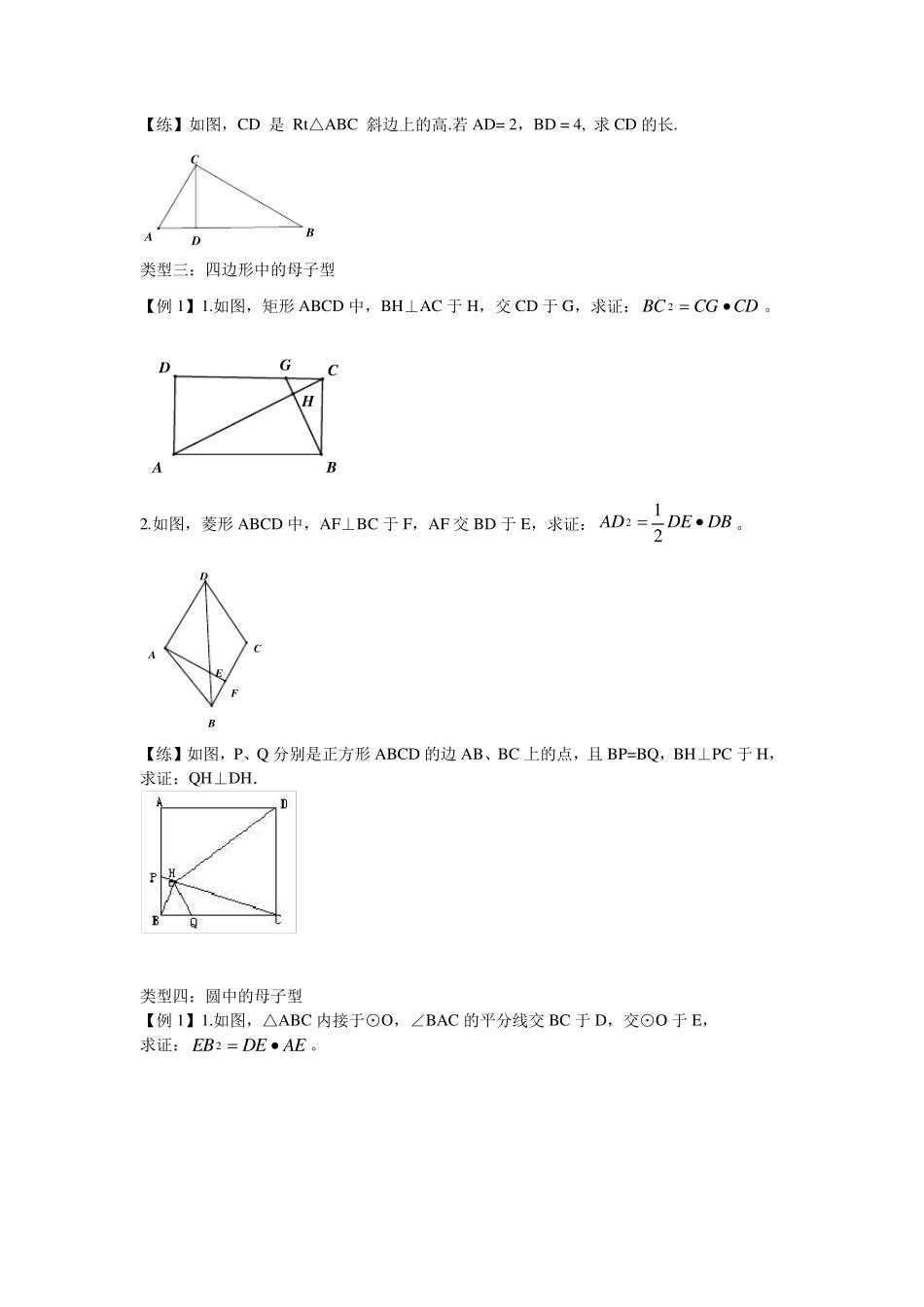
相似三角形之母子三角形 【知识要点】 一、直角三角形相似 1、直角三角形被斜边上的高分成两个直角三角形和原三角形相似。 2、如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。 基本图形(母子三角形)举例: 1、条件:如图,已知△ABC 是直角三角形,CD 为斜边AB 上的高.(射影定理) 结论:(1)△ACD∽△CBD,△BDC∽△BCA,△CDA∽△BCA (2)△ACD∽△CBD 中,2CDAD BD △BDC∽△BCA 中,2BCBD AB △CDA∽△BCA 中,2ACAD AB 2、条件:如图,已知∠ACD=∠ABC(母子) 结论:△ACD∽△ABC 中,2ACAD AB 【例题解析】 类型一:三角形中的母子型 【例1】1.如图,ΔABC 中,∠A=∠DBC,BC=,SΔBCD∶SΔABC=2∶3,则 CD=______. 【练】如图,D 是 △ABC 的边AB 上一点,连结CD.若 AD= 2,BD = 4, ∠ACD =∠B 求AC 的长. 【例2】如图,在△ABC 中,AD 为∠A 的平分线,AD 的垂直平分线交 AD 于 E,交 BC的延长线于 F,求证:FCFBFD2 DCBAADCBADCB 【练】已知CD 是ABC的高,,DECA DFCB,如图3-1,求证:CEFCBA∽ 类型二:直角三角形中的母子型 【例1】.如图,在△ABC 中,AD、BE 分别为BC、AC 边上的高,过D 作AB 的垂线交AB 于F,交BE 于G,交AC 的延长于H,求证:2DFFGFH• 【练】如图5,RtΔ ABC 中,∠ACB=90°,CD⊥AB,AC=8,BC=6,则 AD=____,CD=_______. 【例2】如图1,∠ADC=∠ACB=90°,∠1=∠B,AC=5,AB=6,则 AD=______. HGFEDCBA【练】如图,CD 是 Rt△ABC 斜边上的高.若AD= 2,BD = 4, 求CD 的长. 类型三:四边形中的母子型 【例1】1.如图,矩形ABCD 中,BH⊥AC 于H,交CD 于G,求证:2BCCGCD•。 2.如图,菱形ABCD 中,AF⊥BC 于F,AF 交BD 于E,求证:212ADDEDB•。 【练】如图,P、Q 分别是正方形ABCD 的边AB、BC 上的点,且BP=BQ,BH⊥PC 于H,求证:QH⊥DH. 类型四:圆中的母子型 【例1】1.如图,△ABC 内接于⊙O,∠BAC 的平分线交BC 于D,交⊙O 于E, 求证:2EBDEAE•。 CBADHDACBGEDACBF 2.如图,PA 切⊙O 于A,AB 为⊙O 的直径,M 为PA 的中点,连BM 交⊙O 于C, 求证:(1)2AMM CM B• (2)∠MPC=∠MBP。 【练】1.如图,AB 为⊙O 的直径,CD⊥AB 于D,弧 AC=弧 CE,AE 交CD 于F,求证:2CEAFAE•。...