基本初等函数求导公式VIP免费

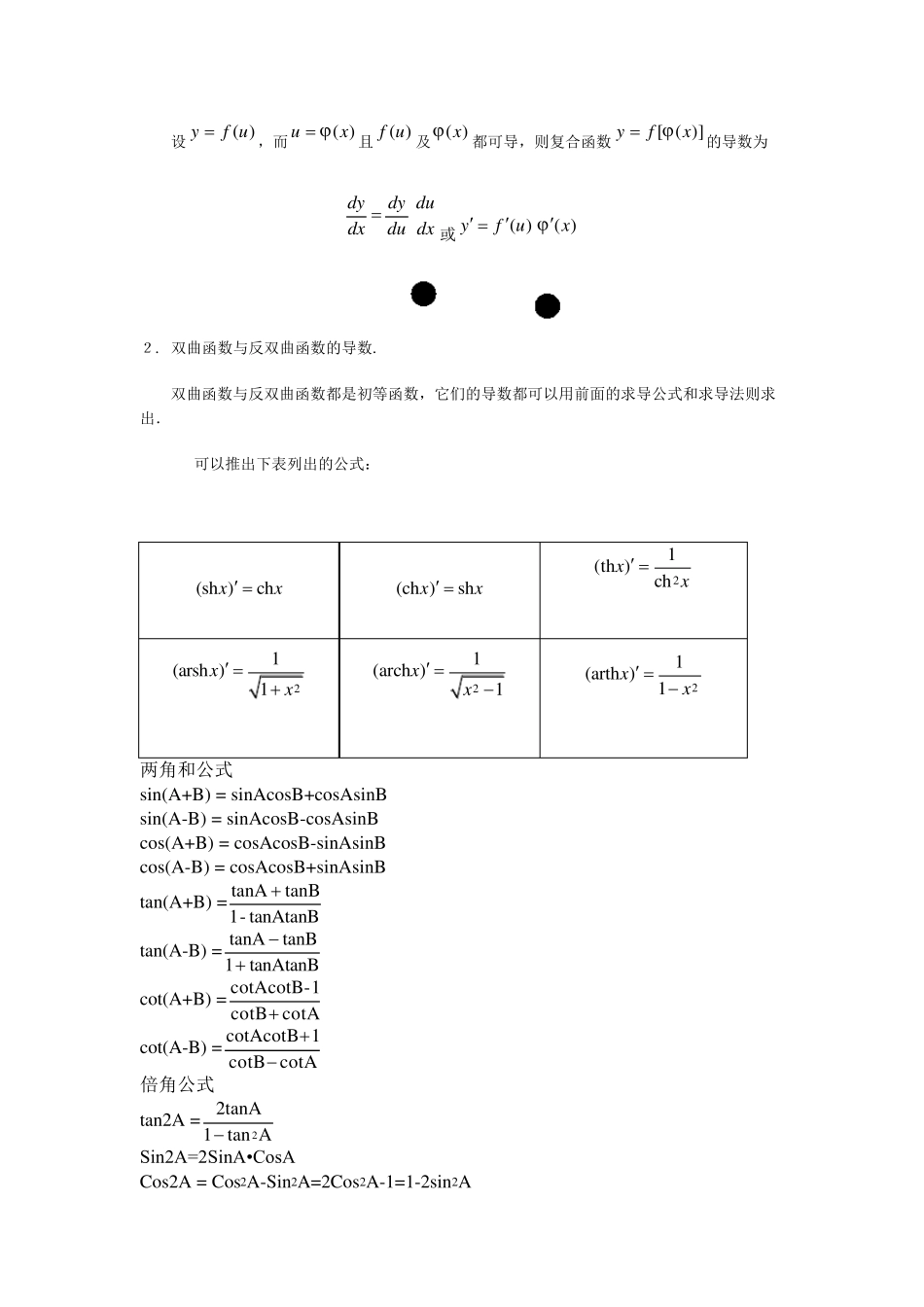
基本初等函数求导公式 (1) 0)(C (2) 1)(xx (3) xxcos)(sin (4) xxsin)(cos (5) xx2sec)(tan (6) xx2csc)(cot (7) xxxtansec)(sec (8) xxxcotcsc)(csc (9) aaaxxln)( (10) (e )exx  (11) axxaln1)(log (12) xx1)(ln， (13) 211)(arcsinxx (14) 211)(arccosxx (15) 21(arctan )1xx   (16) 21(arccot )1xx    函数的和、差、积、商的求导法则 设)(xuu ， )(xvv 都可导，则 （1） vuvu )( （2） uCCu)(（C 是常数） （3） vuvuuv)( （4） 2vvuvuvu 反函数求导法则 若函数)(yx在某区间yI内可导、单调且0)( y，则它的反函数)(xfy 在对应区间xI 内也可导，且 )(1)(yxf 或 dydxdxdy1 复合函数求导法则 设)(ufy ，而)(xu且)(uf及)(x都可导，则复合函数)]([xfy的导数为 dydy dudxdu dx或 ( )( )yfux ２. 双曲函数与反双曲函数的导数. 双曲函数与反双曲函数都是初等函数，它们的导数都可以用前面的求导公式和求导法则求出． 可以推出下表列出的公式： (sh )chxx  (ch )shxx  21(th )chxx  21(arsh )1xx  21(arch )1xx  21(arth )1xx  两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanBtanA  tan(A-B) =tanAtanB1tanBtanA cot(A+B) =cotAcotB1-cotAcotB cot(A-B) =cotAcotB1cotAcotB 倍角公式 tan2A =Atan12tanA2 Sin2A=2SinA•CosA Cos2A = Cos2A-Sin2A=2Cos2A-1=1-2sin2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana·tan( 3 +a)·tan( 3 -a) 半角公式 sin( 2A )=2cos1A cos( 2A )=2cos1A tan( 2A )=AAcos1cos1 cot( 2A )=AAcos1cos1 tan( 2A )=AAsincos1=AAcos1sin 和差化积 sina+sinb=2sin2bacos2ba sina-sinb=2cos2basin2ba cosa+cosb = 2cos2bacos2ba cosa-cosb = -2sin2basin2ba tana+tanb=babacoscos)sin(  积化和差 sinasinb = - 21 ...