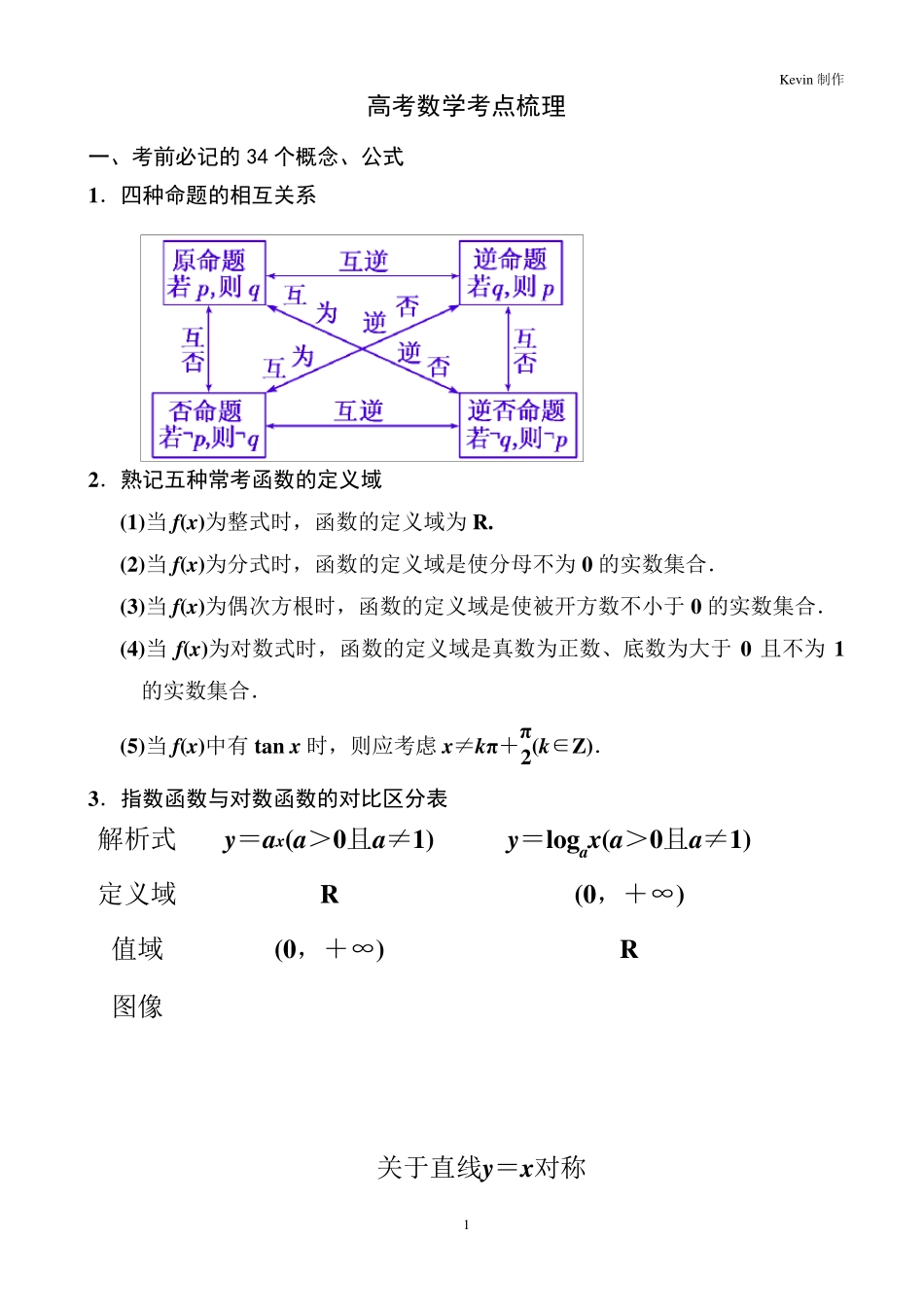
Kev in 制作 1 高考数学考点梳理 一、考前必记的 34 个概念、公式 1.四种命题的相互关系 2.熟记五种常考函数的定义域 (1)当f(x)为整式时,函数的定义域为R. (2)当f(x)为分式时,函数的定义域是使分母不为0 的实数集合. (3)当f(x)为偶次方根时,函数的定义域是使被开方数不小于0 的实数集合. (4)当f(x)为对数式时,函数的定义域是真数为正数、底数为大于0 且不为1的实数集合. (5)当f(x)中有tan x 时,则应考虑x≠kπ+π2(k∈Z). 3.指数函数与对数函数的对比区分表 关于直线y=x对称 图像 R (0,+∞) 值域 (0,+∞) R 定义域 y=logax(a>0且a≠1) y=ax(a>0且a≠1) 解析式 Kev in 制作 2 4.方程的根与函数的零点 (1)方程的根与函数零点的关系: 由函数零点的定义,可知函数y=f(x)的零点就是方程f(x)=0 的实数根,也就是函数y=f(x)的图像与x 轴的交点的横坐标.所以,方程f(x)=0 有实数根⇔函数y=f(x)的图像与x 轴有交点⇔函数y=f(x)有零点. (2)函数零点的存在性: 如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线,并且f(a)·f(b)<0,那么函数f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得f(c)=0,这个c 也就是方程f(x)=0 的实数根. 5.导数公式及运算法则 (1)基本导数公式: C′=0(C 为常数); (xm)′=mxm-1(m∈Q);(sin x)′=cos x; (cos x)′=-sin x;(ex)′=ex; (ax)′=axln a(a>0 且a≠1);(ln x)′=1x; (logax)′ =1xln a(a>0 且a≠1). 0<a<1时,在(0,+∞)上是减函数; a>1 时,在(0,+∞)上是增函数 0<a<1时,在R上是减函数; a>1时,在R上是增 函数 单调性 非奇非偶 非奇非偶 奇偶性 y=logax(a>0且a≠1) y=ax(a>0且a≠1) 解析式 Kev in 制作 3 (2)导数的四则运算: (u± v)′=u′± v′;(uv)′=u′v+uv′;uv ′=u′v-uv′v2(v≠0). (3)复合函数的导数: [f(ax +b)]′=af′(ax+b),如y=sin 2x 有y′=2cos 2x. 6.导数与极值、最值 (1)函数f(x)在x0 处的导数f′(x0)=0 且f′(x)在x0 附近“左正右负”⇔f(x)在x0 处取极大值;函数f(x)在x0 处的导数f′(x0)=0 且f′(x)在x0 附近“左负右正”⇔f(x)在x0 处取极小值. (2)函数f(x)在一闭区间上的最大值是此函数在此区间上的极值与其端点值中的“最大值”;函数f(x)在一闭区间上的...