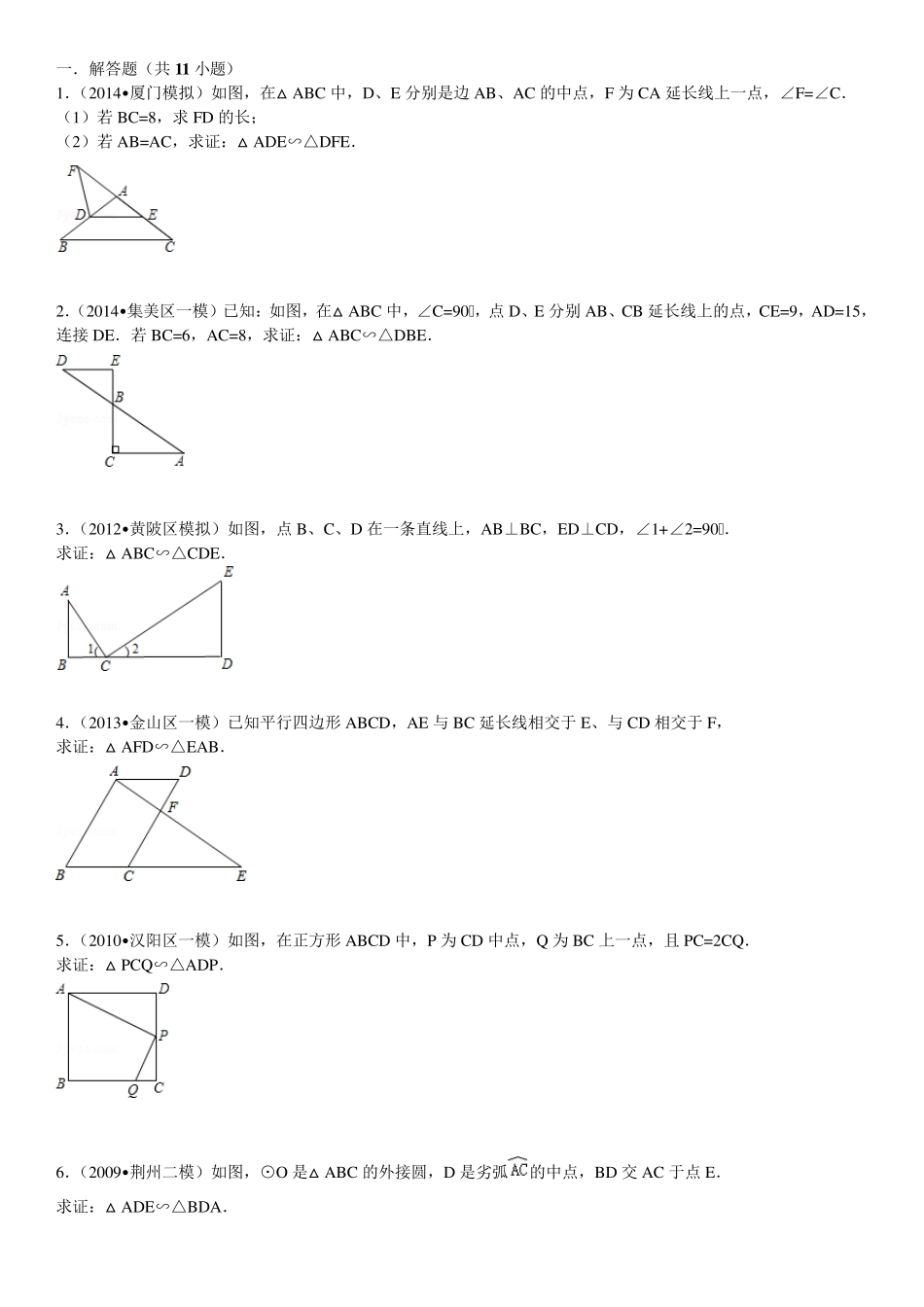
一.解答题(共11 小题) 1.(2014• 厦门模拟)如图,在△ABC 中,D、E 分别是边AB、AC 的中点,F 为CA 延长线上一点,∠F=∠C. (1)若 BC=8,求 FD 的长; (2)若 AB=AC,求证:△ADE∽△DFE. 2.(2014• 集美区一模)已知:如图,在△ABC 中,∠C=90°,点D、E 分别AB、CB 延长线上的点,CE=9,AD=15,连接 DE.若 BC=6,AC=8,求证:△ABC∽△DBE. 3.(2012• 黄陂区模拟)如图,点B、C、D 在一条直线上,AB⊥BC,ED⊥CD,∠1+∠2=90°. 求证:△ABC∽△CDE. 4.(2013• 金山区一模)已知平行四边形 ABCD,AE 与 BC 延长线相交于 E、与 CD 相交于 F, 求证:△AFD∽△EAB. 5.(2010• 汉阳区一模)如图,在正方形 ABCD 中,P 为CD 中点,Q 为BC 上一点,且 PC=2CQ . 求证:△PCQ ∽△ADP. 6.(2009• 荆州二模)如图,⊙O 是△ABC 的外接圆,D 是劣弧的中点,BD 交 AC 于点E. 求证:△ADE∽△BDA. 7.(2007• 莆田)已知:如图,弦AB 和CD 相交于⊙O 内一点P(P 与O 不重合),连接AC,BD,过A 作AE⊥CP于E,过D 作DF⊥PB 于F. (1)请找出图中二对相似三角形: _________ ∽ _________ , _________ ∽ _________ ; (2)请你从(1)中选择一对相似三角形加以证明. 8.(2006• 台州)如图,△ABC 内接于⊙O,∠BAC 的平分线交⊙O 于点D,交边 BC 于点E,连接BD. (1)根据题设条件,请你找出图中各对相似三角形; (2)请选择其中的一对相似三角形加以证明. 9.(1998• 绍兴)已知:如图,△ABC 中,点D、E 分别在 AB、AC 上,DE∥BC,过A、D、C 点的圆交DE 的延长线于F.求证:△FCE∽△ABC. 10.如图所示,已知∠ACB=∠CBD=90°,AC=4cm ,BC=3cm ,那么边 BD 的长度为多少时,△ACB 与△CBD 相似? 11.如图,已知△ABC 内接于⊙O,AE 是⊙O 的直径,AD⊥BC 于D.求证:△ABE∽△ADC. 参考答案与试题解析 一.解答题(共11 小题) 1.(2014• 厦门模拟)如图,在△ABC 中,D、E 分别是边AB、AC 的中点,F 为CA 延长线上一点,∠F=∠C. (1)若 BC=8,求 FD 的长; (2)若 AB=AC,求证:△ADE∽△DFE. 考点: 相似三角形的判定;三角形中位线定理. 分析: (1)利用三角形中位线的性质得出 DE∥BC,进而得出∠AED=∠F,即可得出 FD=DE,即可得出答案; (2)利用等腰...