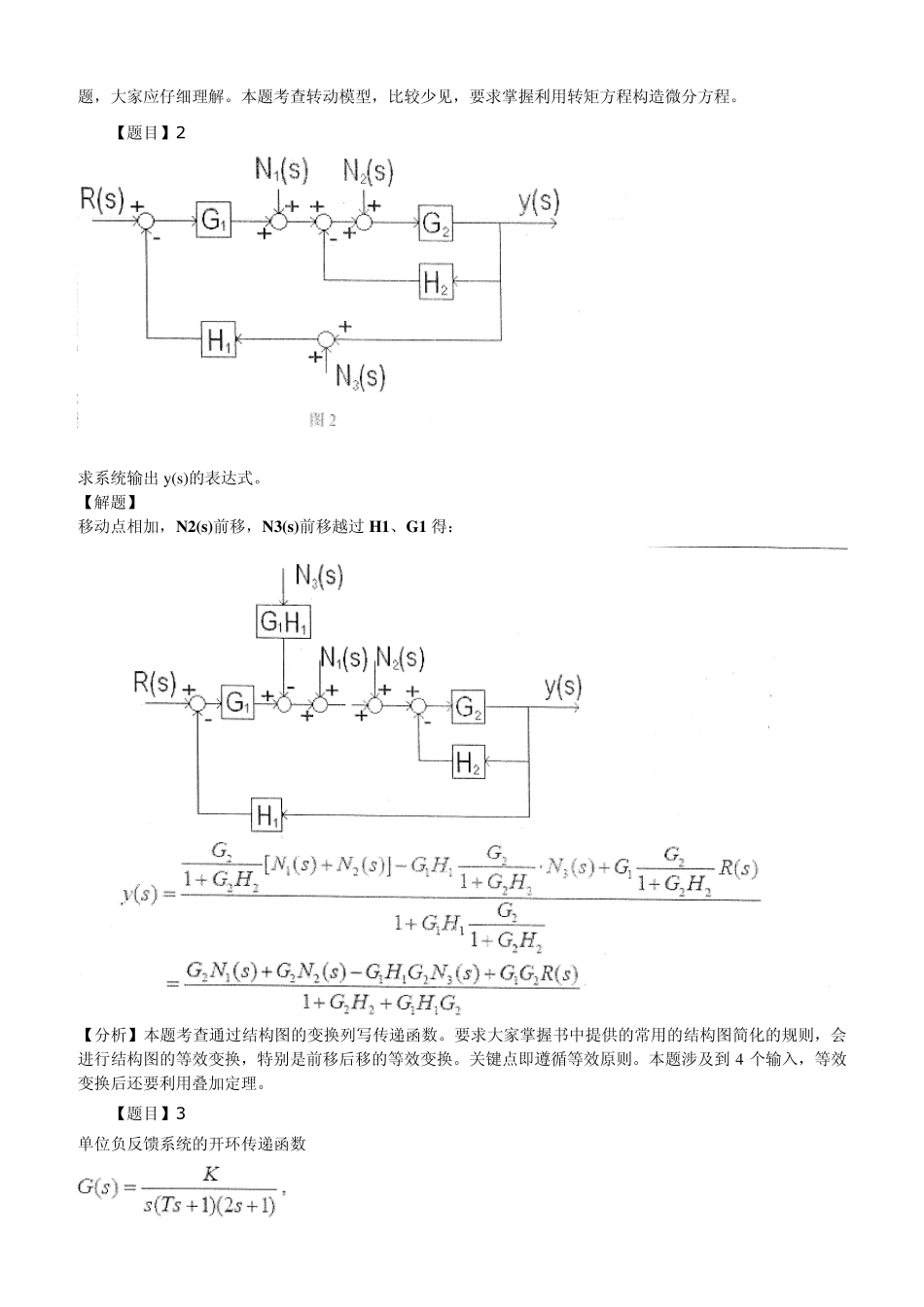
历年试题精讲及答题技巧 通过真题的学习和掌握,可以帮助学生把握考试重点。每年的考点在历年试题中几乎都有重复率,因此,通过对历年真题的把握,可以掌握今年考试的重点。另外,可以通过对历年真题的学习,把握出题者的思路及方法。每种考试都有自己的一种固定的模式和结构,而这种模式和结构很难用语言来表述。而通过认真揣摩历年真题,可以找到这种感觉。因此,第三部分就真题进行详细的剖析,以便考生掌握命题规律、知悉命题的重点、难点、高频考点,帮助考生迅速搭建该学科考试的侧重点和命题规则。 4.1 真题剖析 4.1.1 2007 年真题 【点评】本年份真题包括以下两种题型:判断题,总计 10 分;计算题,总计 140 分;和往年考试题目对比,题型变化很小,其中,题型变化最大的是判断题的出现。 【题目】1 【解题】 【分析】本题考查控制系统的微分方程描述、以及传递函数的转化。要求大家会分析常用的物理规律和化学规律以及拉氏变换。一般常用的模型为电路模型、弹簧模型以及转动模型等。对于三种模型书上均有例题,大家应仔细理解。本题考查转动模型,比较少见,要求掌握利用转矩方程构造微分方程。 【题目】2 求系统输出y(s)的表达式。 【解题】 移动点相加,N2(s)前移,N3(s)前移越过H1、G1 得: 【分析】本题考查通过结构图的变换列写传递函数。要求大家掌握书中提供的常用的结构图简化的规则,会进行结构图的等效变换,特别是前移后移的等效变换。关键点即遵循等效原则。本题涉及到 4 个输入,等效变换后还要利用叠加定理。 【题目】3 单位负反馈系统的开环传递函数 其中K>0, T>0。试求: (1)闭环系统稳定,K 和T 应满足的条件;在K-T 直角坐标系中画出该系统稳定的区域。 (2)若闭环系统处于临界稳定,且振动频率w =1rad/s。求K 和T 的值。 (3)若系统的输入为单位阶跃,分析闭环系统的稳态误差。 解:(1)系统的特征方程为: Routh 判据得,系统稳定: 由K-T 描点,得到曲线: 【分析】本题主要考察线性系统稳定性的分析及稳态误差的计算。要求大家会利用劳斯判据进行线性系统稳定性的判定,掌握劳斯判据的一般情况和特殊情况,以及劳斯判据的应用;掌握稳态误差的计算,会分析不同类型的系统在典型信号作用下的稳态误差。本题从比较新颖的角度考查劳斯判据,但内容仍然为判断稳定、临界稳定的常规内容,大家要注意知识点的区分和串联。 【题目】4 系统结构图如图 4 所示。 (1)...