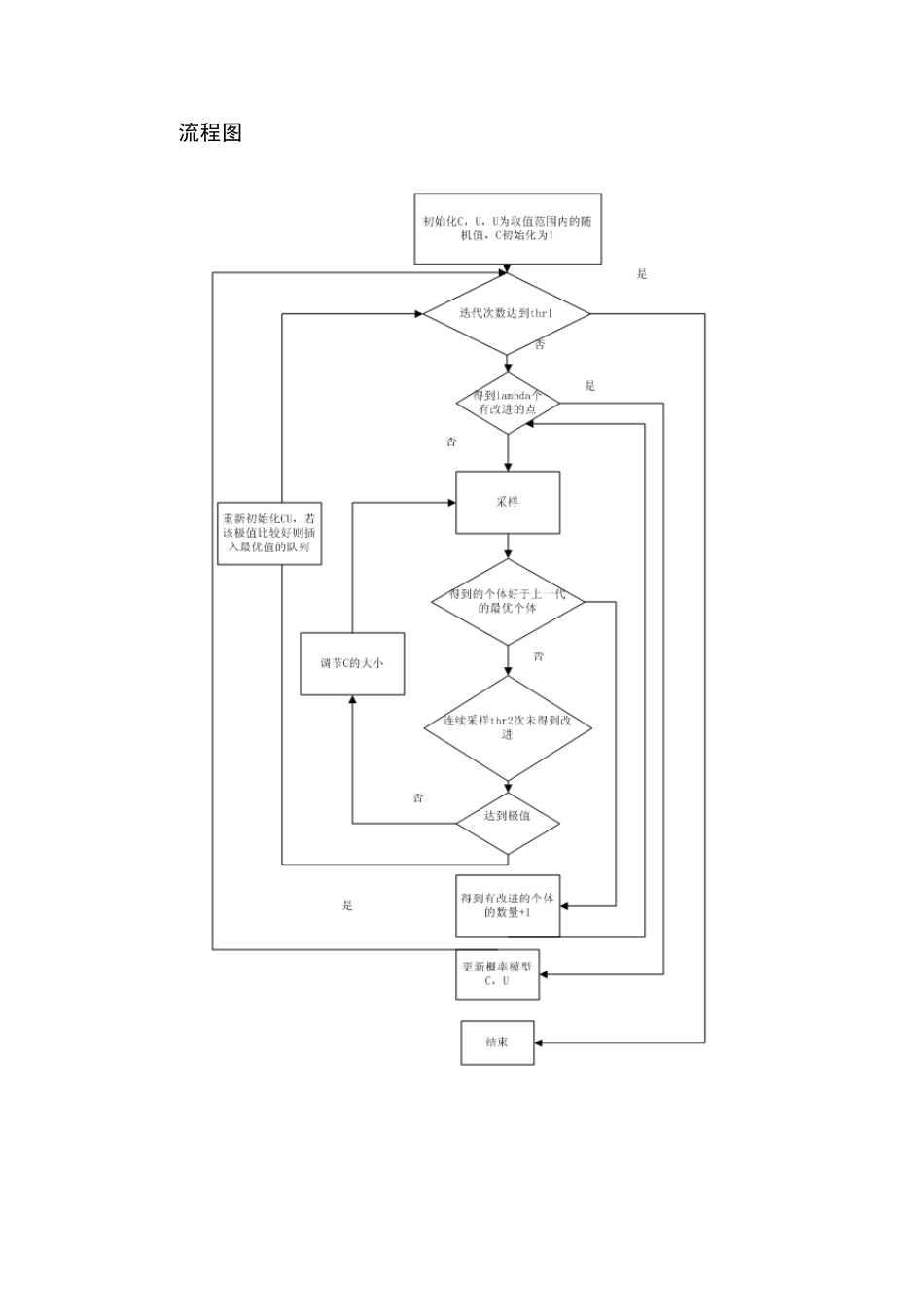
简单的分布估计算法解决连续函数的最优化问题 1 问题描述及求解过程 1.1问题描述 511mincos[(1)]nijijjxj其中-10≤ xi ≤ 10, i=1, 2, … , n. 当 n=1、2、3和 4时分别有 3、18、81和 324 个不同的全局最优解。 1.2问题分析 该问题是一个多峰的连续函数,函数的形式为 )(xif 因此,每一维之间没有相互关系,又因为变量无关的概率模型的学习及采样的过程会比较简单,所以我们采用概率无关的的分布估计算法,函数是连续的,所以我们采用连续域的变量无关的分布估计算法来解决这个问题,求多极值考虑到了两种思路,一种是建立多峰的概率模型,另外一种是建立单峰的概率模型,使之迅速收敛到一个极值,然后再重新初始化模型。由于单峰模型比较简单,所以采用单峰模型。 1.3求解算法策略 分布估计算法遗传算法和统计学习相结合,该算法通过统计学习的方法来更新一个概率模型,并且用这个概率模型来估计解空间有优秀个体的分布情况。通过不断地学习,使得这个概率模型越来越能反映解空间中的优秀个体的分布情况。 分布估计算法的步骤大致可以分为以下两步: 1:构建描述解空间的概率模型.通过对种群的评估,得到优秀的个体集合,然后采用统计学习等手段构造一个描述当前解集的概率模型. 2 :由概率模型随机采样产生新的种群。 要设计一个分布估计算法,首先要考虑到以下三个关键问题 (1):概率模型的选择--对于一个多峰的函数,当然多峰的概率模型有更强的描述能力,但是,多峰的概率模型学习起来比较困难,因此,我们采用一个单峰的概率模型,并使用这个概率模型描述一个局部极值点,当求得一个极值点的时候,重新初始化概率模型,寻找其他的极值点。 单峰的概率模型设计方法 认为每一维都服从一个正态分布即 ),(~iiiCUNx (2):采样以及择优方法--单峰的概率模型很容易陷入到局部最优,因此我们需要不断地重新开始以找到更多的局部最优,在这种情况下,单峰的概率模型收敛越快越好,在这里采用的方法是不断地根据该类模型进行采样,知道采到lambda个个体的适应度要好于当前最好的适应度为止,若连续采样很多次仍没有改进,则需要检测该点是不是极值点,检测的方法是将每一维的d设置成一个较小的值,采样多次,若仍没有改进,则认为该点是极值点。 每一维的采样的方法 iiiUCNx*)1,0( 其中 N(0,1)是一个服从均值为 0,方差为 0.5的正态分布。 (3):概率模型更新方法---根据每次得到...