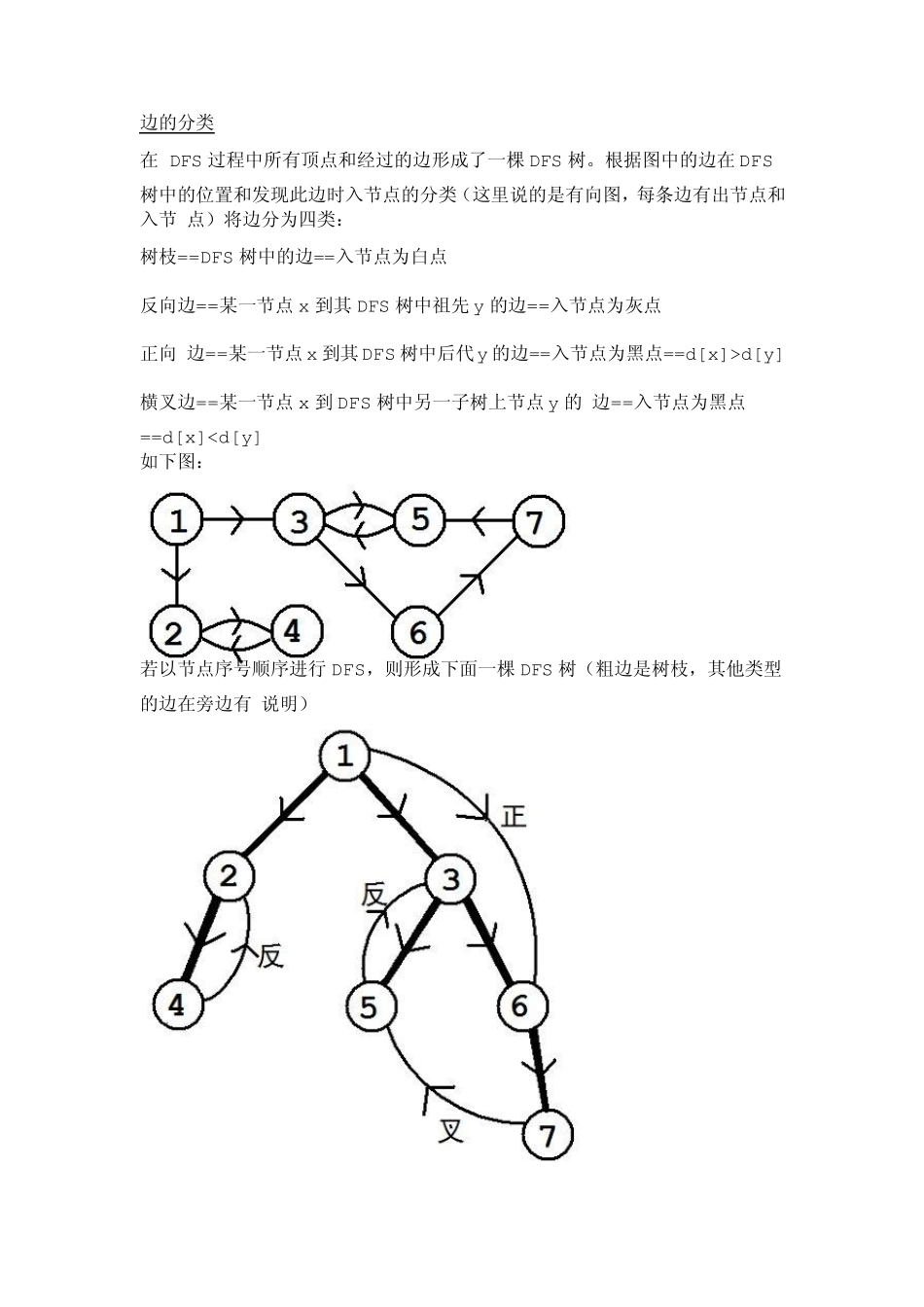
算法学习:有向图的强连通分量 DFS DFS 就是深度 优先搜索,裸的DFS 是很启蒙的一个东西,所以就不废话了,直接给出它的程序: procedu re dfs(x :longint); v ar j:longint; begin flag[x ]:=1; for j:=1 to n do if (a[x ,j]=1)and(flag[j]=0) then dfs(j); end; 其中flag 是是否遍历过的标 记,a 是邻接矩阵。 当然,在主程序中需要有这一句: for i:=1 to n do if flag[i]=0 then dfs(i); 而不是直接的dfs(1),因为节点 1 并不一定能到达所有节点。这是初学者(我?)常犯的一个错误。 当然,DFS 进行的顺 序并不一定是按节点编号顺序。一般按节点编号顺序DFS只是为了方便,有时我们必须以不同的顺序进行 DFS(比如下面将要谈到的Kosaraju 算法)。 时间戳与点的分类 设 置全局变量time,初始值为 0,当遇到一个事件点的时候就++1。时间点分为两种:发现某一节点和结束某一节点(即在 DFS 过程的开头和结尾)。发现节 点 x 时,发现时间戳 d[x]=time;结束节点 x 时,结束时间戳 f[x]=time。 根据时间戳状态的不同可以将节点进行分类: 白 点==没有时间戳的节点==未遍历的节点 灰点==仅有发现时间戳的节点==正在遍历以此节点为根的子树的节点 黑点==有发现时间戳和结束 时间戳的节点==完成的节点 注意:点的分类随 time 增长而变化,且 DFS 结束后所有点都是黑点,所以用一个全局变量保存点的分类没有意义。 DFS 过程中可以直接通过时间戳得知点的分类。 边的分类 在 DFS 过程中所有顶点和经过的边形成了一棵DFS 树。根据图中的边在DFS树中的位置和发现此边时入节点的分类(这里说的是有向图,每条边有出节点和入节 点)将边分为四类: 树枝==DFS 树中的边==入节点为白点 反向边==某一节点x 到其 DFS 树中祖先 y 的边==入节点为灰点 正向 边==某一节点x 到其DFS 树中后代y 的边==入节点为黑点==d[x]>d[y] 横叉边==某一节点x 到 DFS 树中另一子树上节点y 的 边==入节点为黑点==d[x]