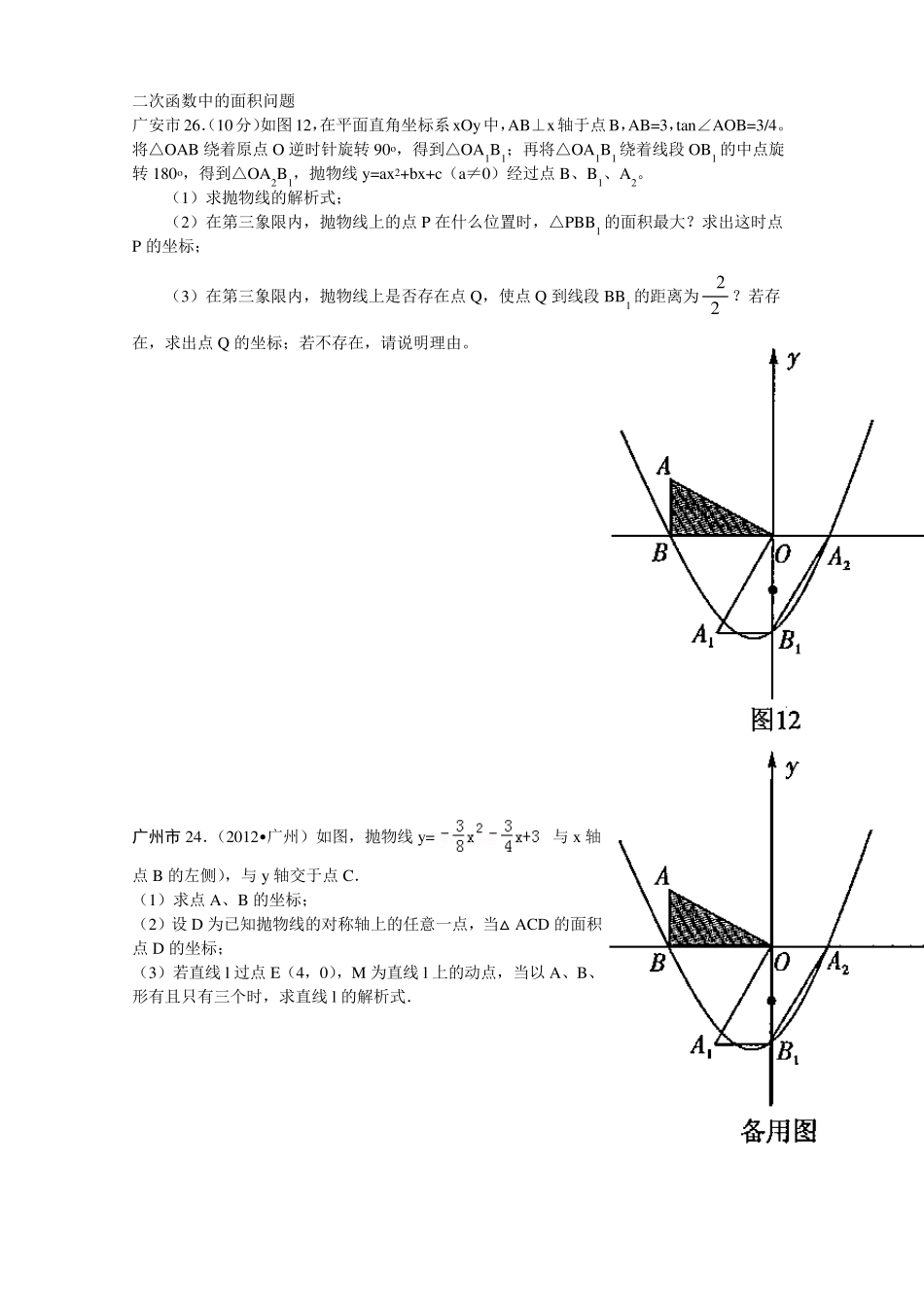
二次函数中的面积问题 广安市26.(10 分)如图12,在平面直角坐标系x Oy 中,AB⊥x 轴于点B,AB=3,tan∠AOB=3/4。将△OAB 绕着原点O 逆时针旋转 90o,得到△OA1B1;再将△OA1B1 绕着线段 OB1 的中点旋转 180o,得到△OA2B1,抛物线 y =ax 2+bx +c(a≠0)经过点B、B1、A2。 (1)求抛物线的解析式; (2)在第三象限内,抛物线上的点P 在什么位置时,△PBB1 的面积最大?求出这时点P 的坐标; (3)在第三象限内,抛物线上是否存在点Q,使点Q 到线段 BB1 的距离为 22?若存在,求出点Q 的坐标;若不存在,请说明理由。 广州市 24.(2012• 广州)如图,抛物线 y =与 x 轴交于A、B 两点(点A 在点B 的左侧),与 y 轴交于点C. (1)求点A、B 的坐标; (2)设 D 为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB 的面积时,求点D 的坐标; (3)若直线 l 过点E(4,0),M 为直线 l 上的动点,当以 A、B、M 为顶点所作的直角三角形有且只有三个时,求直线 l 的解析式. 广东省22. 如图,抛物线923212xxy与x 轴交于A、B 两点,与y 轴交于点C,连接BC、AC。 (1)求AB 和OC 的长; (2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A、B 不重合)。过点E 作直线l 平行BC,交AC 于点D。设AE 的长为m,△ADE 的面积为s,求s 关于m 的函数关系式,并写出自变量m的取值范围; (3)在(2)的条件下,连接CE,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留 )。 黔东南州24、如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)D三点。 (1)、求抛物线的解析式。 (2)、点M是线段BC上的点(不与B,C重合),过M作MN∥ y 轴交抛物线于N若点M 的横坐标为m ,请用 m 的代数式表示 MN的长。 (3)、在(2)的条件下,连接NB、NC,是否存在点m ,使△BNC的面积最大?若存在,求m 的值,若不存在,说明理由。 y A O B x E l C D 题 22 图 y A O B x E l C D 题 22 图 黔西南州26、如图11,在平面直角坐标系x Oy 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线的对称轴l 与x 轴相交于点M. (1)求抛物线对应的函数解析式和对称轴; (2)设点P 为抛物线(x >5)上的一点,若以A、O、M、P 为顶点的四边形的四条边的长度为四个连续的正整数,...