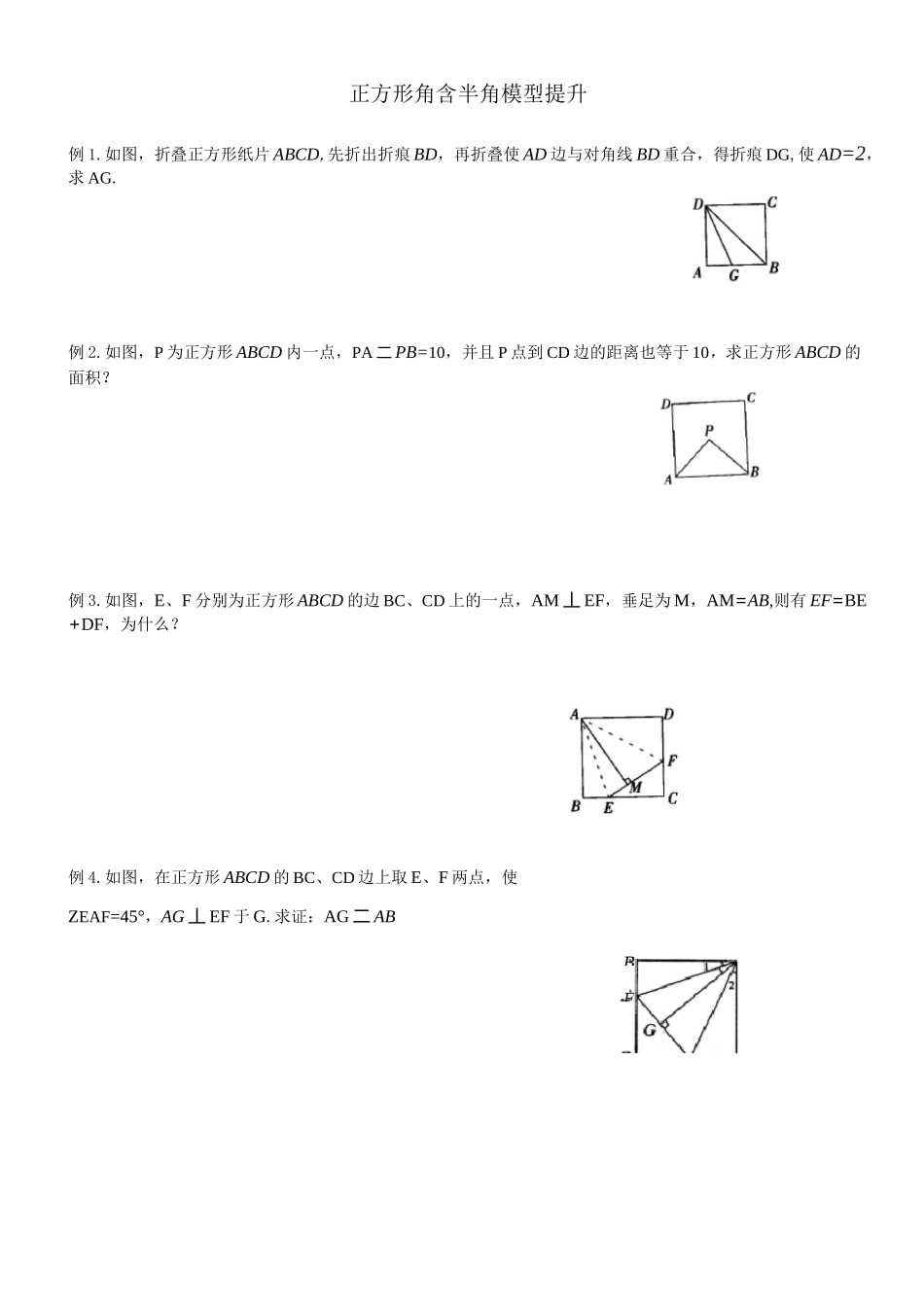
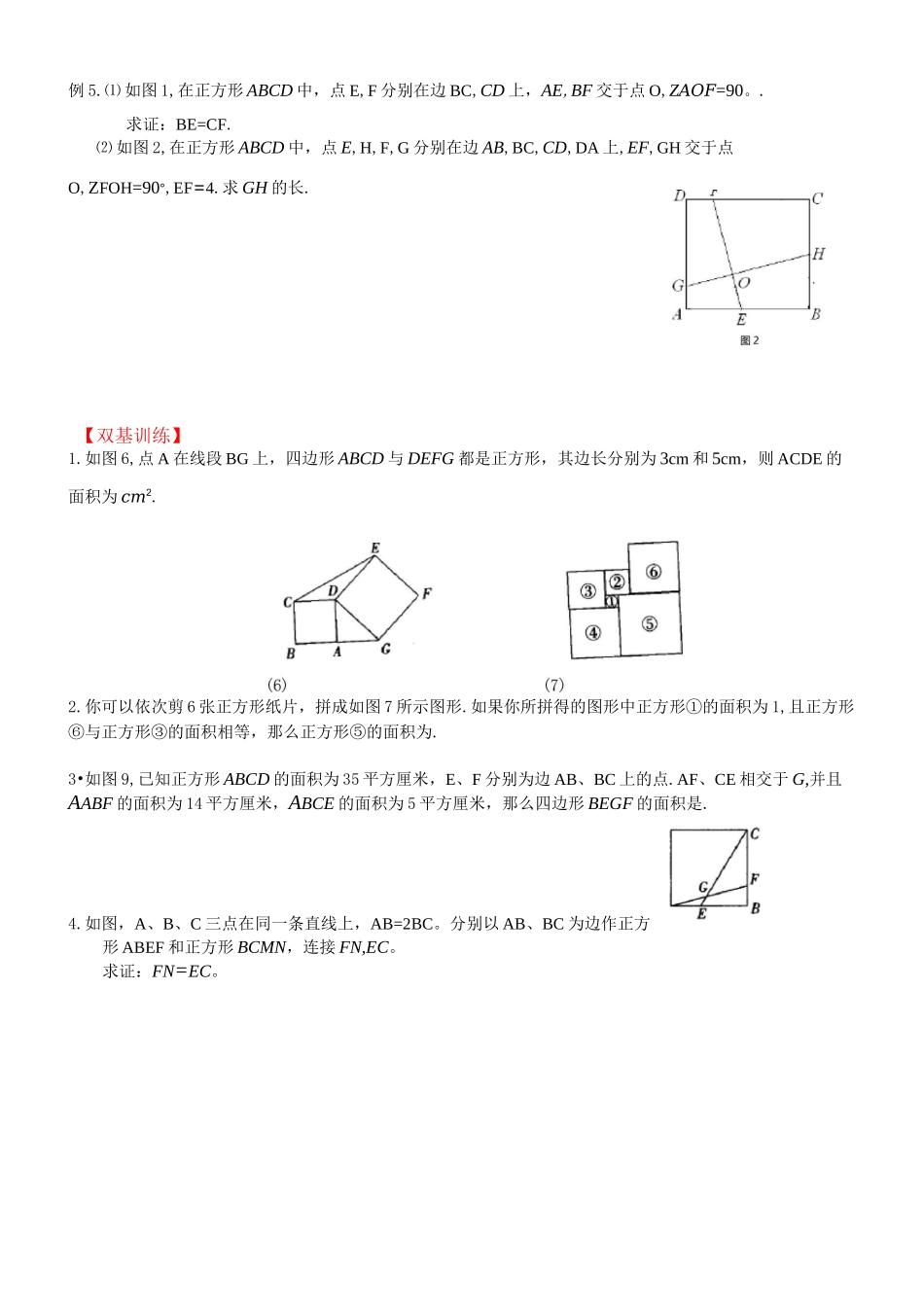
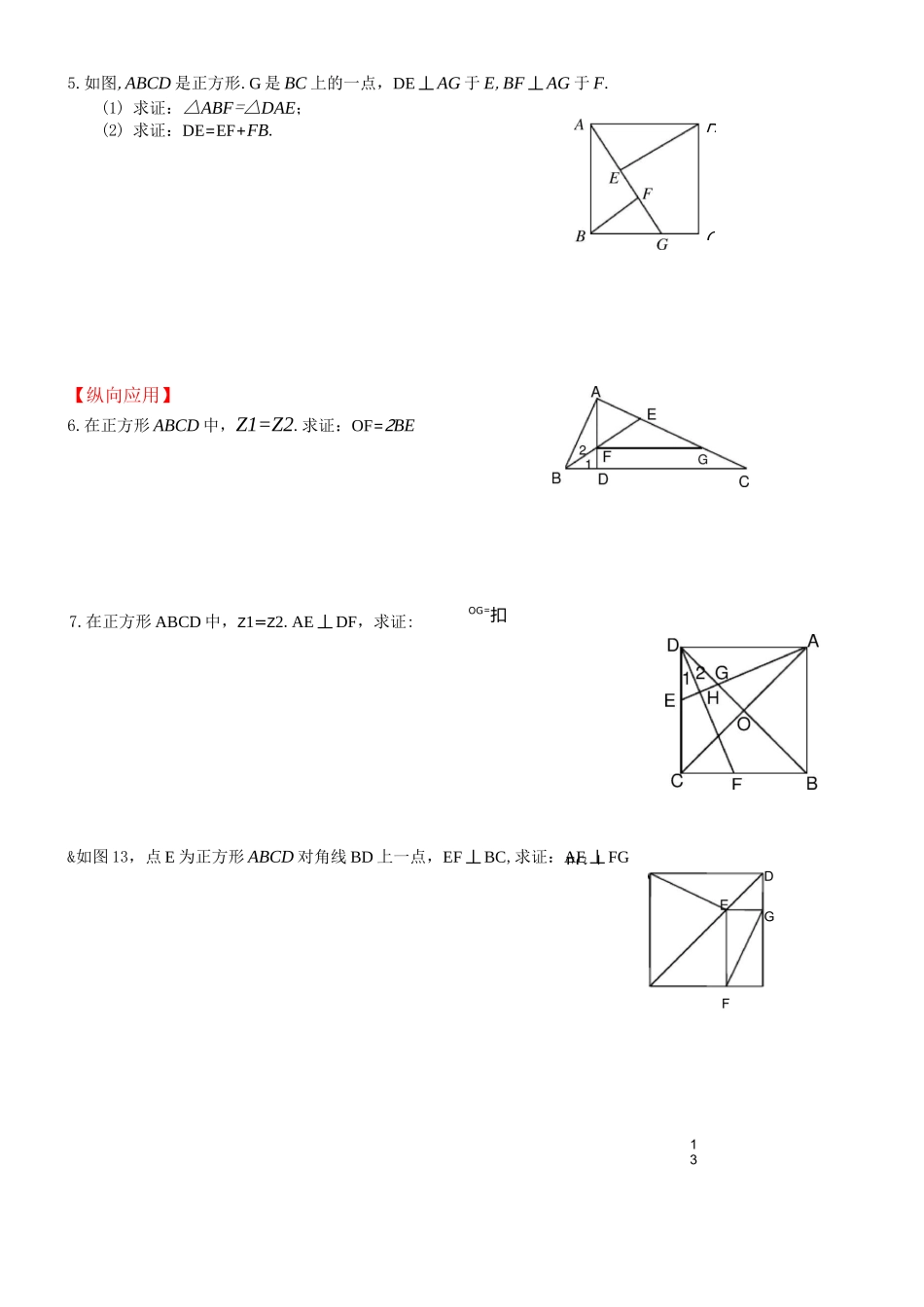
正方形角含半角模型提升例 1.如图,折叠正方形纸片 ABCD,先折出折痕 BD,再折叠使 AD 边与对角线 BD 重合,得折痕 DG,使 AD=2,求 AG.例 2.如图,P 为正方形 ABCD 内一点,PA 二 PB=10,并且 P 点到 CD 边的距离也等于 10,求正方形 ABCD 的面积?例 3.如图,E、F 分别为正方形 ABCD 的边 BC、CD 上的一点,AM 丄 EF,垂足为 M,AM=AB,则有 EF=BE+DF,为什么?例 4.如图,在正方形 ABCD 的 BC、CD 边上取 E、F 两点,使ZEAF=45°,AG 丄 EF 于 G.求证:AG 二 ABBE例 5.⑴ 如图 1,在正方形 ABCD 中,点 E,F 分别在边 BC,CD 上,AE,BF 交于点 O,ZAOF=90。.求证:BE=CF.⑵ 如图 2,在正方形 ABCD 中,点 E,H,F,G 分别在边 AB,BC,CD,DA 上,EF,GH 交于点O,ZFOH=90°,EF=4.求 GH 的长.【双基训练】1.如图 6,点 A 在线段 BG 上,四边形 ABCD 与 DEFG 都是正方形,其边长分别为 3cm 和 5cm,则 ACDE 的面积为 cm2.2.你可以依次剪 6 张正方形纸片,拼成如图 7 所示图形.如果你所拼得的图形中正方形①的面积为 1,且正方形⑥与正方形③的面积相等,那么正方形⑤的面积为.3•如图 9,已知正方形 ABCD 的面积为 35 平方厘米,E、F 分别为边 AB、BC 上的点.AF、CE 相交于 G,并且AABF 的面积为 14 平方厘米,ABCE 的面积为 5 平方厘米,那么四边形 BEGF 的面积是.4.如图,A、B、C 三点在同一条直线上,AB=2BC。分别以 AB、BC 为边作正方形 ABEF 和正方形 BCMN,连接 FN,EC。求证:FN=EC。13EG 丄5.如图,ABCD 是正方形.G 是 BC 上的一点,DE 丄 AG 于 E,BF 丄 AG 于 F.(1) 求证:△ABF=△DAE;(2) 求证:DE=EF+FB.【纵向应用】6.在正方形 ABCD 中,Z1=Z2.求证:OF=2BE&如图 13,点 E 为正方形 ABCD 对角线 BD 上一点,EF 丄 BC,求证:AE 丄 FGDC7.在正方形 ABCD 中,Z1=Z2.AE 丄 DF,求证:OG=扣DGF边,在 AABC 的外侧作正方形 ACDE 和正方形 CBFG,点 P 是 EF半.9•已知:点 E、F 分别正方形 ABCD 中 AB 和 BC 的中点,连接 AF 和 DE 相交于点 G,GH丄 AD 于点 H.(1) 求证:AF 丄 DE;(2) 如果 AB=2,求 GH 的长;(3) 求证:CG 二 CD例 1.已知:如图,P 是正方形 ABCD 内点,ZPAD=ZPDA=15。.求证:APBC 是正三角形.例 2.如图,分别以 AABC 的 AC 和 BC 为的中点.求...