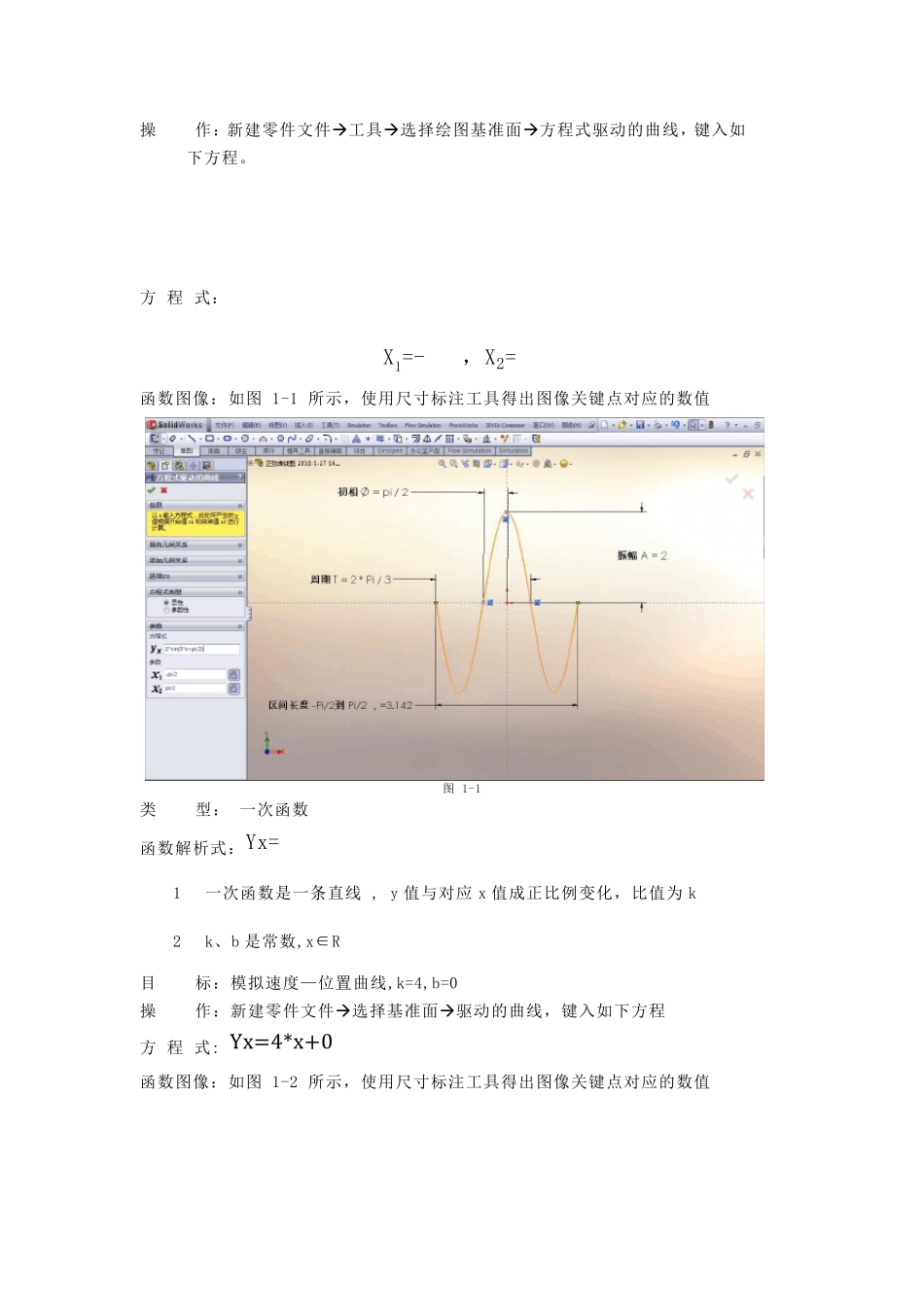
SolidWorks 中 “ 方 程 式 驱 动 的 曲 线 ” 工 具 的 应 用 潘 思 达 SolidWords 自 从2007 版 开 始 , 草 图 绘 制 工 具 中 添 加 了 “ 方 程 式 驱 动 的 曲 线 ” 工具 , 用 户 可 通 过 定 义 ” 笛 卡 尔 坐 标 系 ” (暂 时 还 不 支 持 其 他 坐 标 系 ) 下 的 方 程 式 来 生成 你 所 需 要 的 连 续 曲 线 。 这 种 方 法 可 以 帮 助 用 户 设 计 生 成 所 需 要 的 精 确 的 数 学 曲 线 图形 , 目 前 可 以 定 义 “ 显 式 的 ” 和 “ 参 数 的 ” 两 种 方 程 式 。 本 文 将 分 别 依 次 介 绍 这 两 种方 程 式 的 定 义 方 法 , 以 及 绘 制 一 些 特 殊 曲 线 时 的 注 意 事 项 。 “ 显 式 方 程 ” 在 定 义 了 起 点 和 终 点 处 的 X 值 以 后 , Y 值 会 随 着 X 值 的 范 围 而自 动 得 出 ; 而 “ 参 数 方 程 ” 则 需 要 定 义 曲 线 起 点 和 终 点 处 对 应 的 参 数 (T)值 范 围 , X值 表 达 式 中 含 有 变 量 T, 同 时 为Y 值 定 义 另 一 个 含 有T 值 的 表 达 式 , 这 两 个 方 程 式 都会 在T 的 定 义 域 范 围 内求解, 从 而 生 成 需 要 的 曲 线 。 下 面介 绍 一 下 笛 卡 尔 坐 标 系 下 常用 的 一 些 曲 线 的 定 义 方 法 ,通 过 图 片可 以 看出 所绘 制 曲 线 的 关键位置的 数 值 。 对 于有 些 在 其 他 坐 标 系 下 定 义 的 曲 线 方 程 , 例如极坐 标系 方 程 ,大家可 以 使用 基本 的 数 学 方 法 先将 该坐 标 系 下 的 曲 线 方 程 转化到笛 卡 尔 坐 标系 以 后 就可 以 重新定 义 该曲 线 了 。 关于“ 方 程 式 曲 线 ” 对 话框其 他 的 选项 功能大家可 以 参 照SolidWords 帮 助 文 件详细了 解使用 方 法 。 (一 )显 式 方 程 类 型: 正弦函数 函数 解析式 : 1 正弦曲 线 是一 条波浪线 , k、ω和 φ是常数 (k、ω、φ∈R, ω≠0) 2 A——振幅、(ωx+φ)——相位、φ——初相 3 k—...