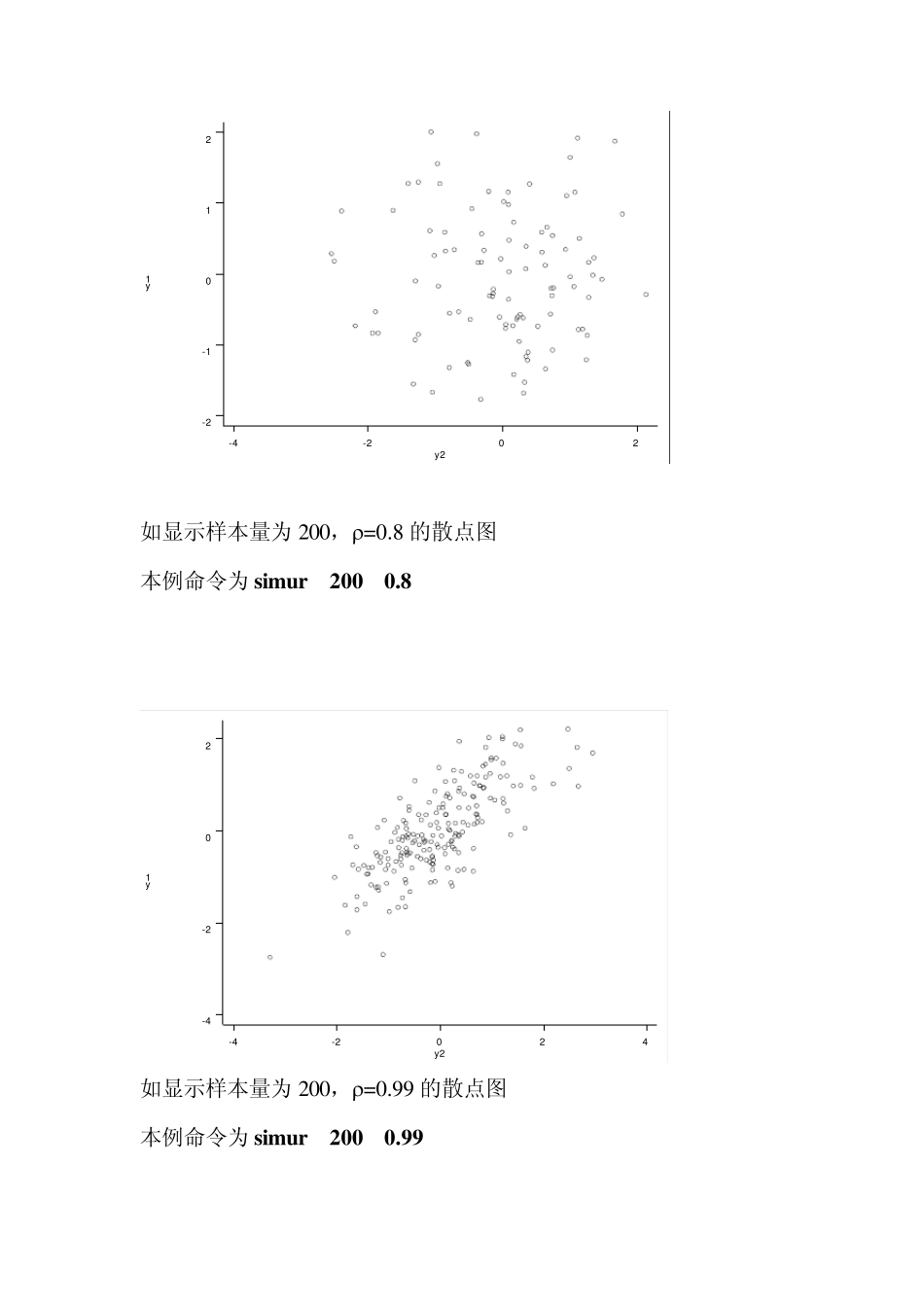
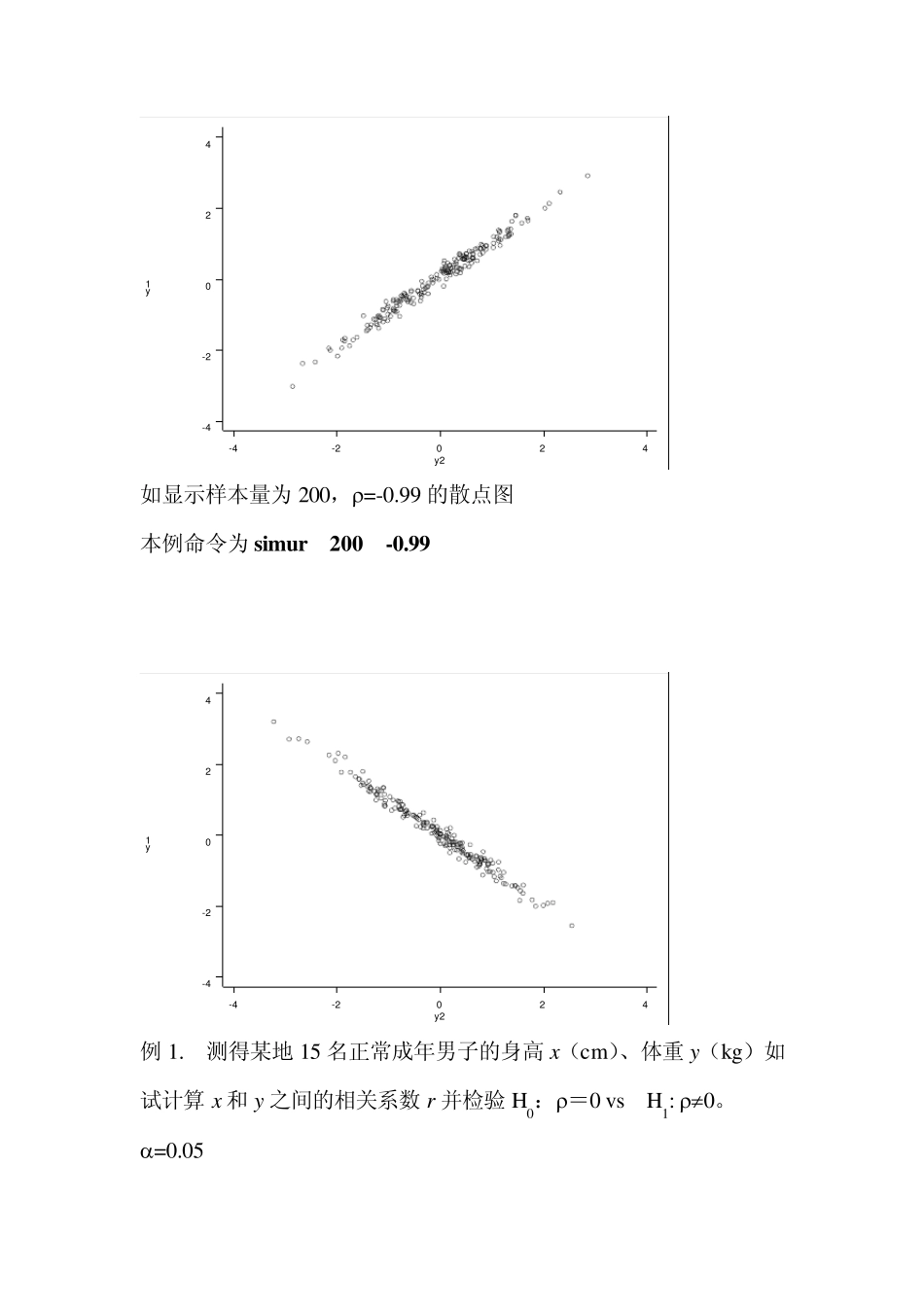
线性相关和回归 赵耐青 在实际研究中,经常要考察两个指标之间的关系,即:相关性。现以体重与身高的关系为例,分析两个变量之间的相关性。要求身高和体重呈双正态分布,既:在身高和体重平均数的附近的频数较多,远离身高和体重平均数的频数较少。 样本相关系数计算公式(称为 Pearson 相关系数): )()())((22YYXXXYLLLYYXXYYXXr (1) 1. 考察随机模拟相关的情况。 显示两个变量相关的散点图程序 simur.ado(本教材配套程序,使用见前言)。命令为 simur 样本量 总体相关系数 如显示样本量为 100,=0 的散点图 本例命令为 simu r 100 0 如显示样本量为 200,=0.8 的散点图 本例命令为 simu r 200 0.8 y1y2-4-2024-4-202 如显示样本量为 200,=0.99 的散点图 本例命令为 simu r 200 0.99 y1y2-4-202-2-1012y1y2-4-2024-4-2024 如显示样本量为200,=-0.99 的散点图 本例命令为simu r 200 -0.99 y1y2-4-2024-4-2024 例1. 测得某地15 名正常成年男子的身高x(cm)、体重 y(kg)如试计算 x 和 y 之间的相关系数 r 并检验 H0:=0 vs H1: 0。 =0.05 数据格式为 X Y 171.0 58.0 176.0 69.0 175.0 74.0 172.0 68.0 170.0 64.0 173.0 68.5 168.0 56.0 172.0 54.0 170.0 62.0 172.0 63.0 173.0 67.0 168.0 60.0 171.0 68.0 172.0 76.0 173.0 65.0 Stata 命令 pwcorr 变量1 变量2 … 变量m,sig 本例命令 pwcorr x y,sig pwcorr x y,sig | x y -------------+------------------ x | 1.0000 | | y | 0.5994 1.0000 | 0.0182 | Pearson 相关系数=0.5994,P 值=0.0182<0.05,因此可以认为身高与体重呈正线性相关。 注意:Pearson 相关系数又称为线性相关系数并且要求X 和Y 双正态分布,通常在检查中要求X 服从正态分布并且Y 服从正态分布。 如果不满足双正态分布时,可以计算Spearman 相关系数又称为非参数相关系数。 Spearman 相关系数的计算基本思想为:用X 和Y 的秩代替它们的原始数据,然后代入Pearson 相关系数的计算公式并且检验与Pearson相关系数类同。 Stata 实现 spearman x y Number of obs = 15 Spearman's rho = 0.6552 Test of Ho: x and y are independent Prob > |t| = 0.0080 stata 计算结果与手算的结果一致。结论为身高与体...