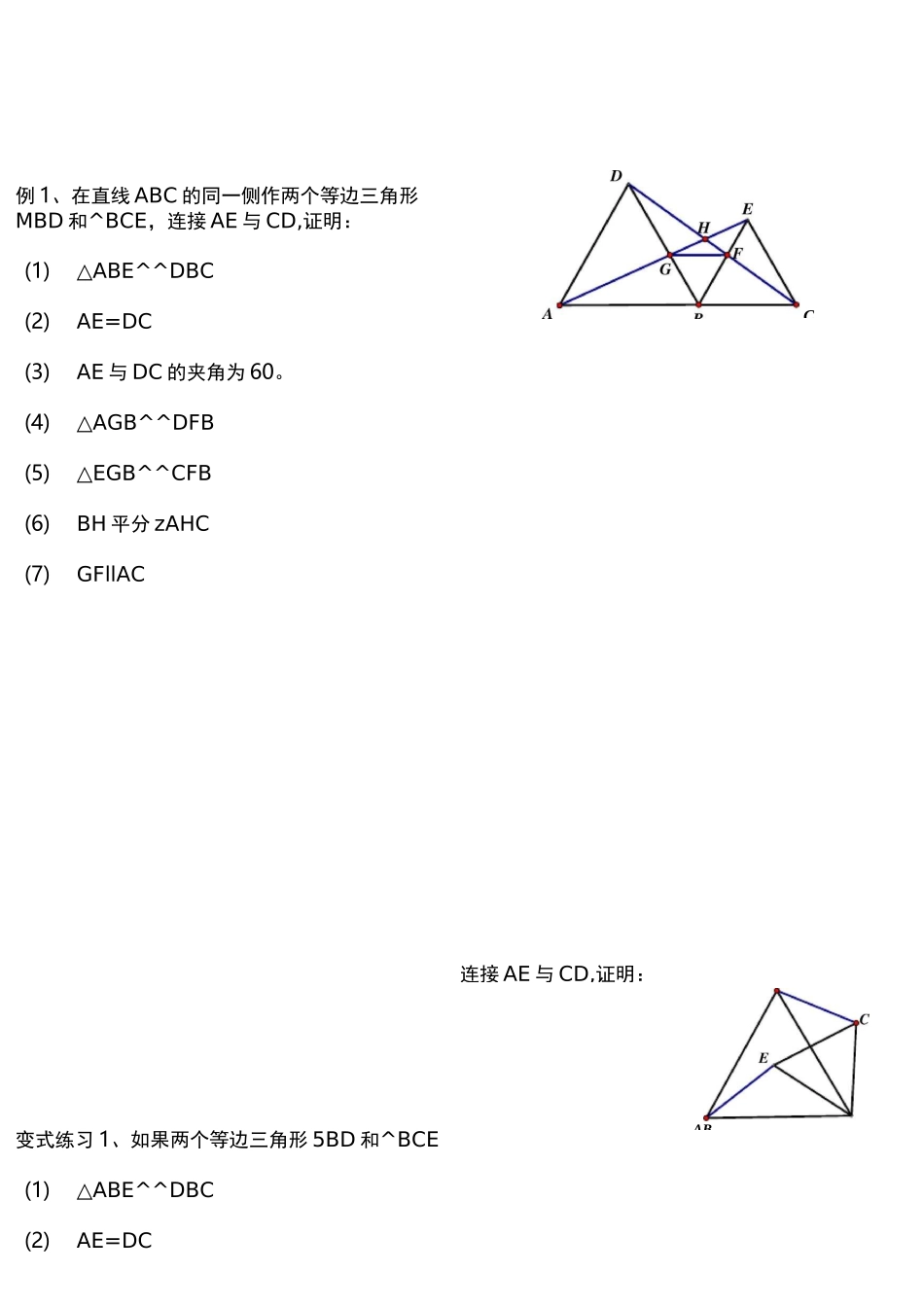
'003壮、廿ffl©J06溜。06®@-崔®川H帅®舉、。09憾09®@--is(I)(SB®)asJft7(q丄“)画<=(-is(CN)c丄)回«TIj國连接 AE 与 CD,证明:例 1、在直线 ABC 的同一侧作两个等边三角形MBD 和^BCE,连接 AE 与 CD,证明:(1)△ABE^^DBC(2)AE=DC(3)AE 与 DC 的夹角为 60。(4)△AGB^^DFB(5)△EGB^^CFB(6)BH 平分 zAHC(7)GFllAC变式练习 1、如果两个等边三角形 5BD 和^BCE(1)△ABE^^DBC(2)AE=DCCAB(3)AE 与 DC 的夹角为 60。(4)AE 与 DC 的交点设为 H,BH 平分 zAHC变式练习 2、如果两个等边三角形 3BD 和^BCE,连接 AE 与 CD,证明:(1RABE 妥^DBC(2)AE=DC⑶AE 与 DC 的夹角为 60。(4)AE 与 DC 的交点设为 H,BH 平分 zAHC(1)如图 1,点 C 是线段 AB 上-点,分别以 AC,BC 为边在 AB 的同侧作等边 MCM 和 MBN,连接AN,BM.分别取 BM,AN 的中点 E,F,连接 CE,CF,EF.观察并猜想 MEF 的形状,并说明理由.(2)若将(1)中的“以 AC,BC 为边作等边 3CM 和 MBN”改为“以 AC,BC 为腰在 AB 的同侧作等腰MCM 和 MBN”如图 2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由.N2 半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。例 1、如图,正方形 ABCD 的边长为 1,AB,AD 上各存在一点 P、Q,若 3PQ 的周长为 2,求 ZPCQ 的度数。例 2、在正方形 ABCD 中,若 M、N 分别在边 BC、CD 上移动,且满足 MN=BM+DN,求证:① zMAN=45。;②AfnMxNn8△CMN 的周长=2AB:③AM、AN 分别平分 zBMN 和 zDNM。例 3、在正方形 ABCD 中,已知 zMAN=45。,若 M、N 分别在边 CB、DC 的延长线上移动:①试探究线段 MN、BM、DN 之间的数量关系;②求证:AB=AH.例 4、在四边形 ABCD 中,zB+zD=180°,AB 二 AD,若 E、F 分别在边 BC、CD 且上,满足 EF 二BE+DF.求证:ZEAF=1ABAD。24、已知:如图 1 在 R1MSC 中「兰£4 匚=蒯,=r点比 E 分别为线段丑匚上两动点’若乂口匹=45°,探究埃段加、应、氐三条线段之间的数量关系.沪明的思路是:把吐证匚绕点刖蒯针旋转眇,得到的 E'「瞬 FD,使问题得到解决■请你参考小明的思路探^并解决下列问题:⑴ 猜想甜、DE、.£■匸三条线段之间存在的数量关蔡式 r并对你也青想给予证明;② 当动点王在统段眈上.动点。运动在线段 CB 延长找上时.如图 2.其它案件不娈.⑴ 中探究的结论星否发生改变?请说匪你的常想并给予证明‘