二次方程根的分布情况归纳VIP免费

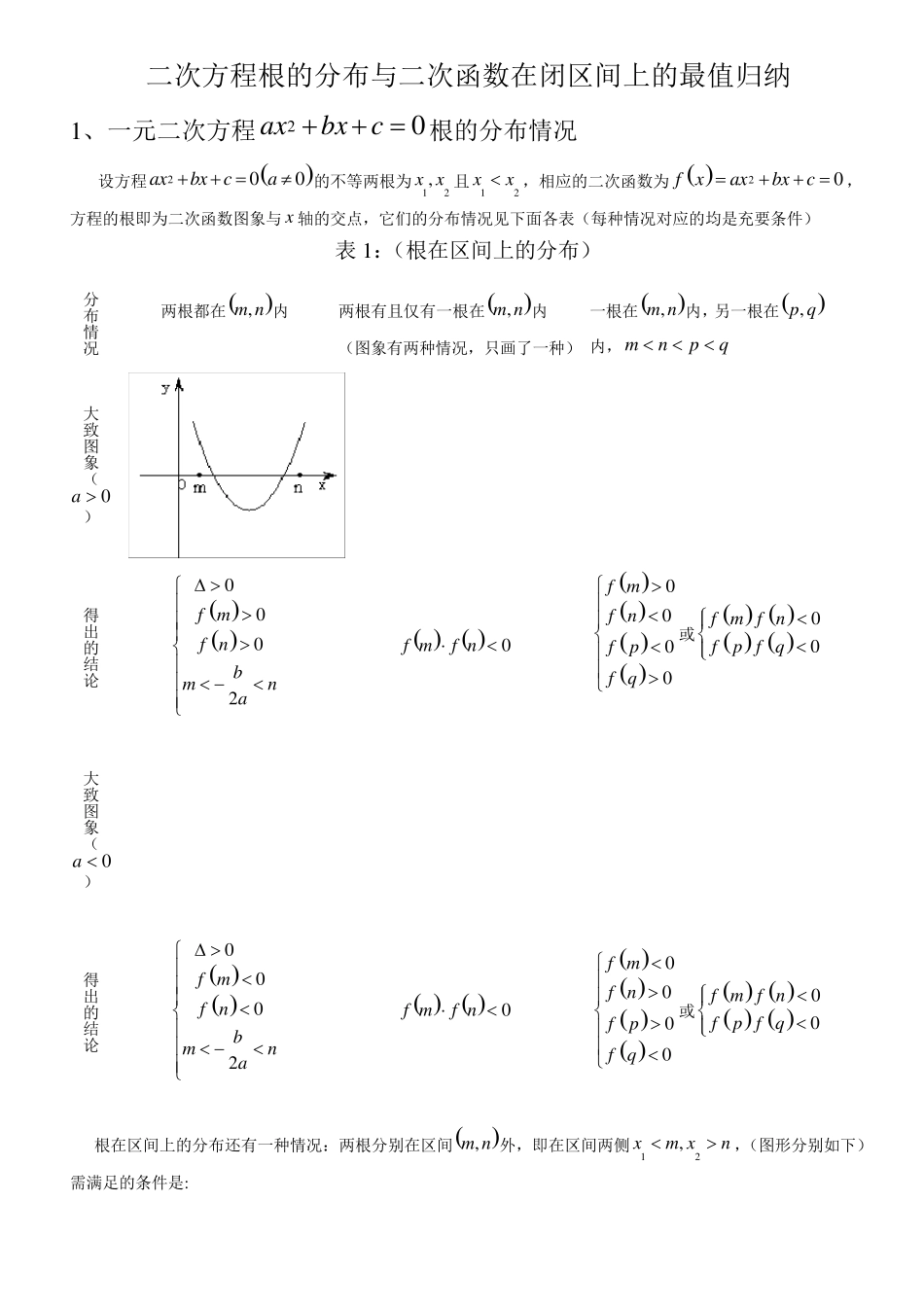
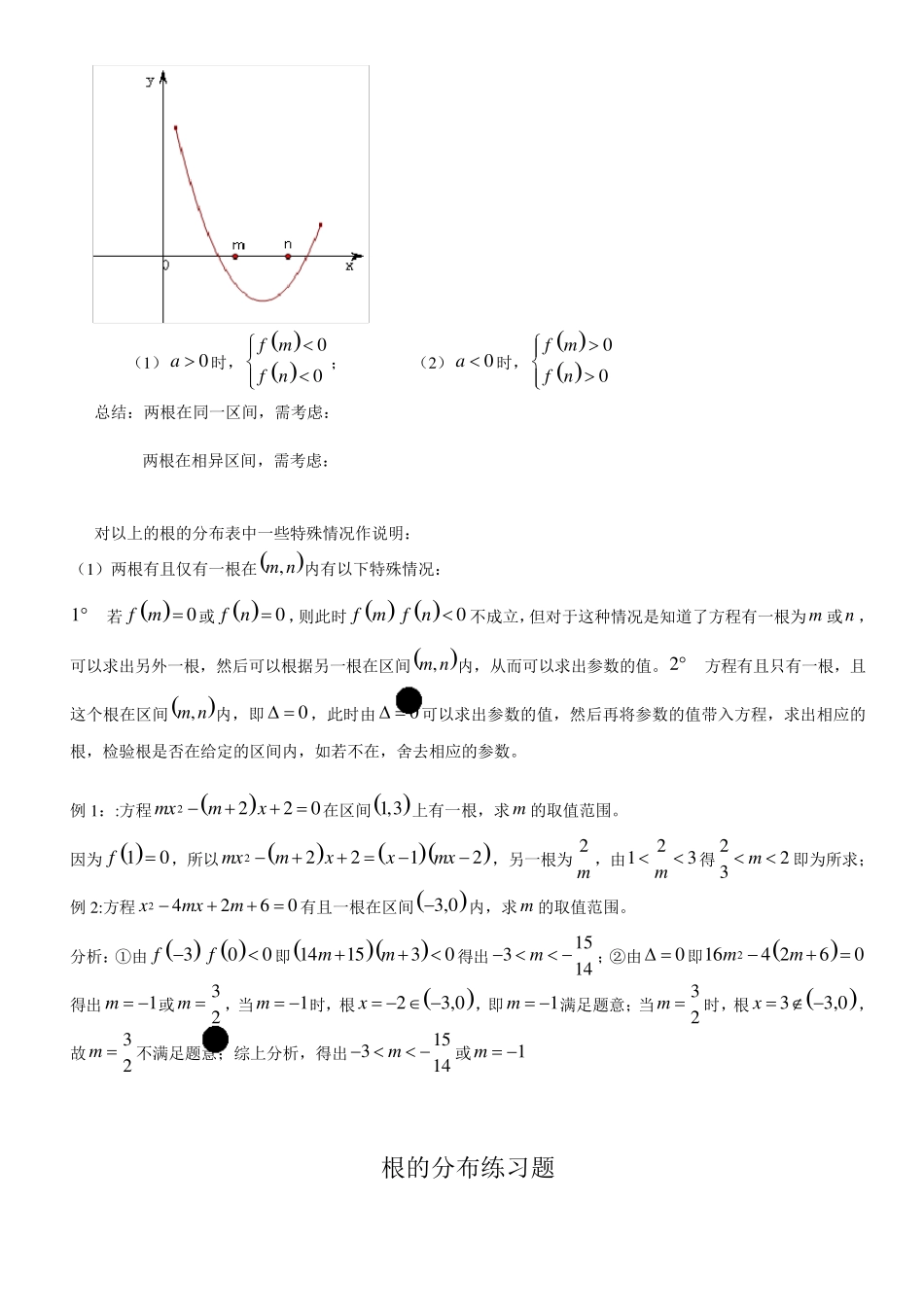
二次方程根的分布与二次函数在闭区间上的最值归纳 1、一元二次方程02cbxax根的分布情况 设方程200axbx ca 的不等两根为12,x x 且12xx，相应的二次函数为  20f xaxbxc，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件） 表 1：（根在区间上的分布） 分布情况 两根都在nm,内 两根有且仅有一根在nm,内 （图象有两种情况，只画了一种） 一根在nm,内，另一根在qp,内，qpnm 大致图象（0a） 得出的结论   0002f mf nbmna     0nfmf     0000f mf nfpf q或      00f m f nfp f q 大致图象（0a） 得出的结论   0002f mf nbmna     0nfmf     0000f mf nfpf q或      00f m f nfp f q 根在区间上的分布还有一种情况：两根分别在区间nm,外，即在区间两侧12,xm xn，（图形分别如下）需满足的条件是: （1）0a 时，  00f mf n； （2）0a 时，  00f mf n 总结：两根在同一区间，需考虑： 两根在相异区间，需考虑： 对以上的根的分布表中一些特殊情况作说明： （1）两根有且仅有一根在nm,内有以下特殊情况： 1 若 0f m 或 0f n ，则此时   0f mf n 不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间nm,内，从而可以求出参数的值。2 方程有且只有一根，且这个根在区间nm,内，即0 ，此时由0 可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数。 例1：:方程2220mxmx在区间1,3 上有一根，求m 的取值范围。 因为 10f，所以22212mxmxxmx，另一根为2m ，由213m得223m即为所求； 例2:方程24260xmxm有且一根在区间3,0内，求m 的取值范围。 分析：①由   300ff...