初三数学中考复习第一轮—函数专题之二次函数(教案)VIP免费

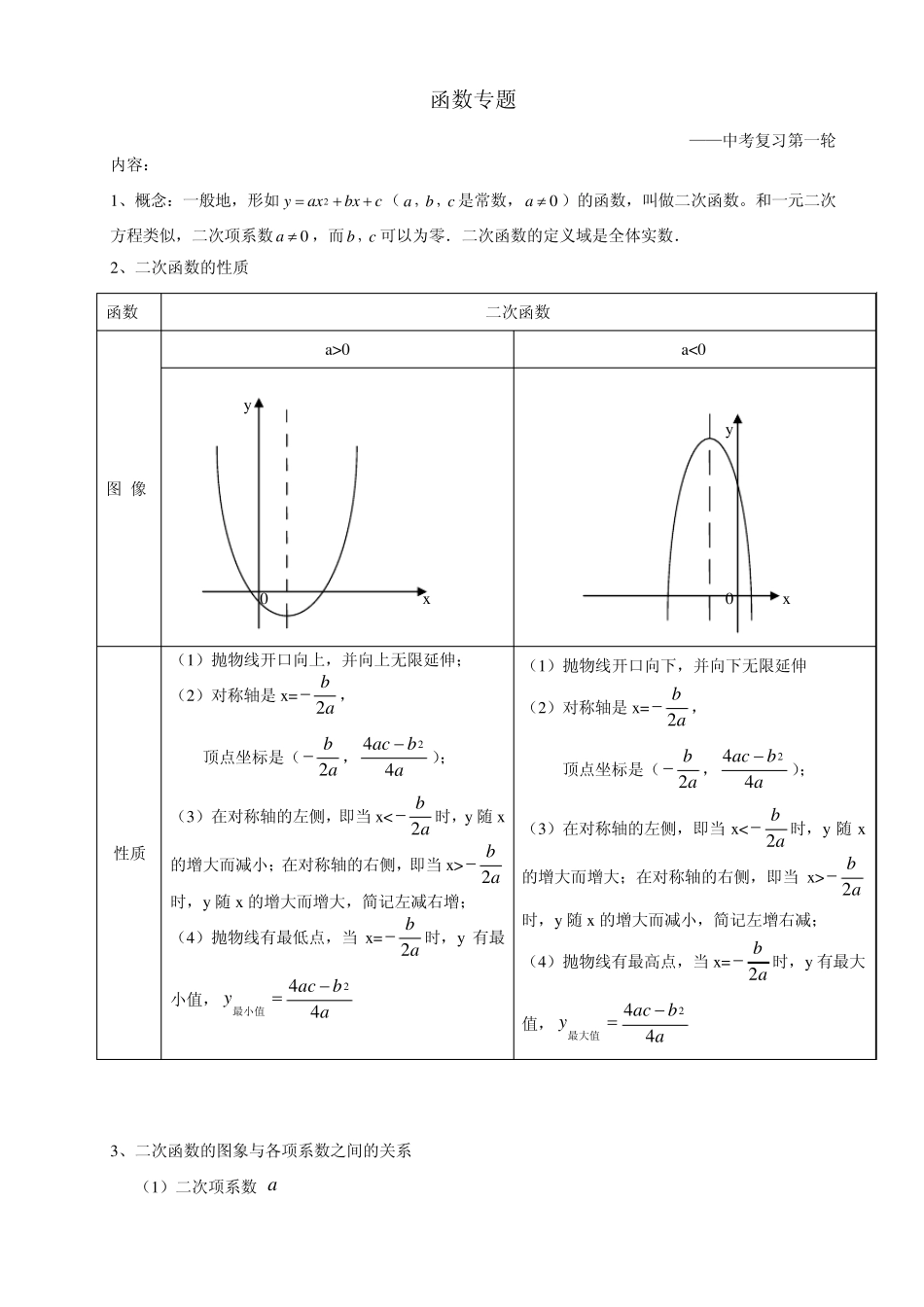
函数专题 ——中考复习第一轮 内容： 1、概念：一般地，形如2yaxbxc （ abc， ， 是常数，0a ）的函数，叫做二次函数。和一元二次方程类似，二次项系数0a ，而 bc， 可以为零．二次函数的定义域是全体实数． 2、二次函数的性质 3、二次函数的图象与各项系数之间的关系 （1）二次项系数 a 函数 二次函数 图 像 a>0 a<0 y 0 x y 0 x 性质 （1）抛物线开口向上，并向上无限延伸； （2）对称轴是 x=ab2， 顶点坐标是（ab2，abac442）； （3）在对称轴的左侧，即当 xab2时，y 随 x 的增大而增大，简记左减右增； （4）抛物线有最低点，当 x=ab2时，y 有最小值，abacy442最小值 （1）抛物线开口向下，并向下无限延伸 （2）对称轴是 x=ab2， 顶点坐标是（ab2，abac442）； （3）在对称轴的左侧，即当 xab2时，y 随 x 的增大而减小，简记左增右减； （4）抛物线有最高点，当 x=ab2时，y 有最大值，abacy442最大值 a 决定抛物线开口的大小和方向，a ＞0，抛物线开口向上，a ＜0，抛物线开口向下； a 的大小决定开口的大小，a 越小开口越大。 （2）ba和共同决定抛物线的对称轴： aby2 （3）c 是抛物线与y 轴交点的纵坐标。 4、二次函数图象的平移 ① 将抛物线解析式转化成顶点式2ya xhk，确定其顶点坐标hk，； ② 保持抛物线2yax的形状不变，将其顶点平移到hk，处，具体平移方法如下： 向右(h>0)【或左(h<0)】平移 |k|个单位向上(k>0)【或下(k<0)】平移|k|个单位向右(h>0)【或左(h<0)】平移|k|个单位向右(h>0)【或左(h<0)】平移|k|个单位向上(k>0)【或下(k<0)】平移|k|个单位向上(k>0)【或向下(k<0)】平移|k|个单位y=a(x-h)2+ky=a(x-h)2y=ax 2+ky=ax2 ③ 图像平移步骤 （1）配方2()ya xhk，确定顶点（h,k） （2）对x 轴 左加右减；对y 轴 上加下减 例：将抛物线 22xy 的图像先向右平移2 个单位看，再向上平移3 个单位后，得到的抛物线的解析式是 3222 xy 5、.用待定系数法求二次函数的解析式 (1)一般式：cbxaxy2. 已知图像上三点或三对x 、y 的值，通常选择一般式. (2)顶点式：khxay2. 已知图像的顶点或对称轴，通常选择顶点式. (3...