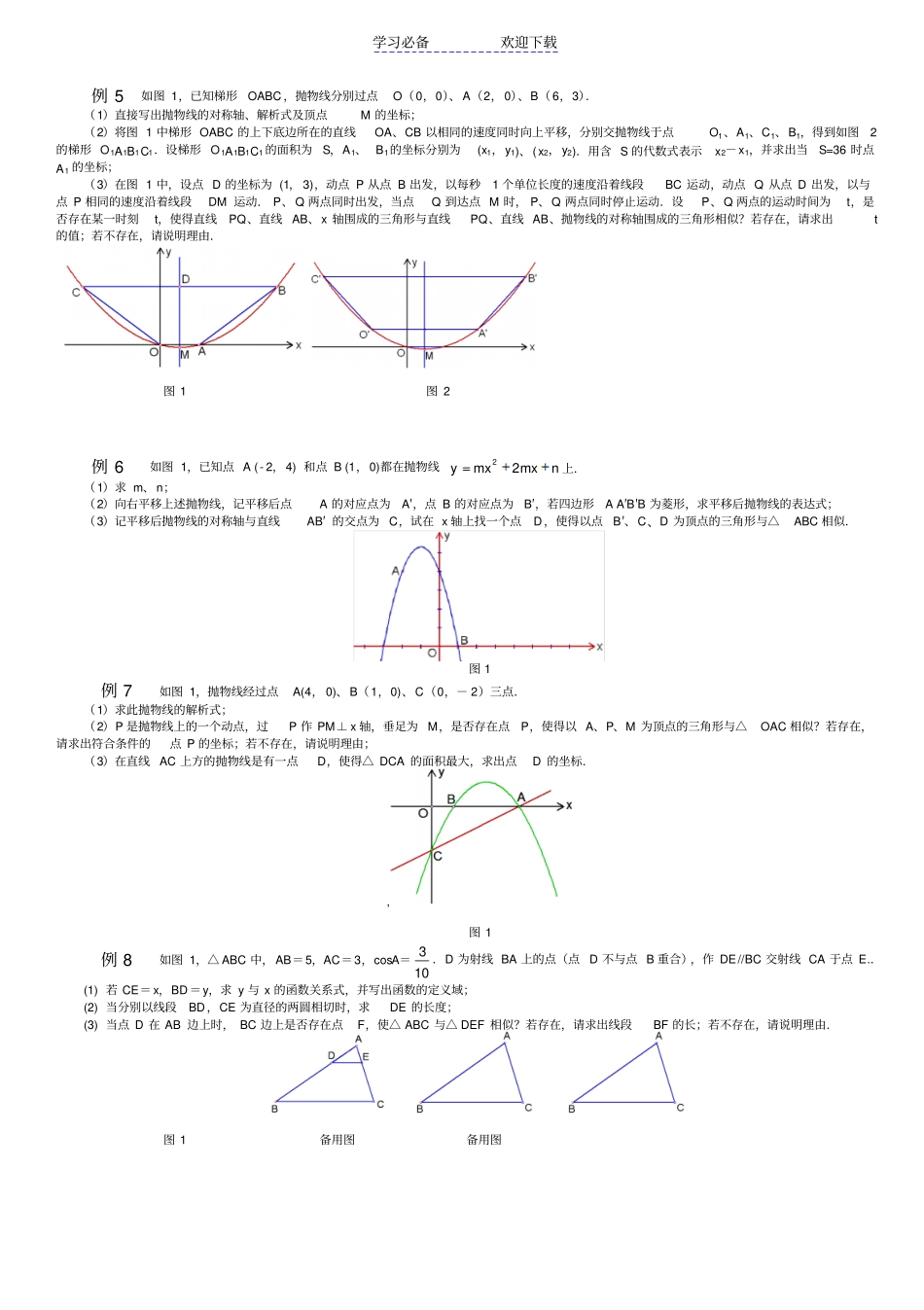
学习必备欢迎下载第一部分函数图象中点的存在性问题1.1 因动点产生的相似三角形问题 1如图 1,已知抛物线211 (1)444byxbx(b 是实数且 b>2)与 x 轴的正半轴分别交于点A、B(点 A 位于点 B 是左侧),与 y 轴的正半轴交于点C.(1)点 B 的坐标为 ______,点 C 的坐标为 __________(用含 b 的代数式表示) ;(2)请你探索在第一象限内是否存在点P,使得四边形PCOB 的面积等于2b,且△ PBC 是以点 P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;(3)请你进一步探索在第一象限内是否存在点Q,使得△ QCO 、△ QOA 和△ QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.图 1 例 2 如图 1,已知抛物线的方程C1:1 (2)()yxxmm(m>0)与 x 轴交于点B、C,与 y 轴交于点 E,且点 B 在点 C 的左侧.(1)若抛物线C1 过点 M(2, 2),求实数 m 的值;(2)在( 1)的条件下,求△BCE 的面积;(3)在( 1)的条件下,在抛物线的对称轴上找一点H,使得 BH+ EH 最小,求出点H 的坐标;(4)在第四象限内,抛物线C1 上是否存在点F,使得以点B、C、F 为顶点的三角形与△BCE 相似?若存在,求m 的值;若不存在,请说明理由.图 1 例 3 直线113yx分别交 x 轴、 y 轴于 A、B 两点, △AOB 绕点 O 按逆时针方向旋转90°后得到 △COD ,抛物线 y=ax2+bx+ c 经过 A、C、D 三点.(1) 写出点 A、B、C、D 的坐标;(2) 求经过 A、C、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线 BG 上是否存在点Q,使得以点A、B、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.图 1例 4 Rt△ABC 在直角坐标系内的位置如图1 所示,反比例函数(0)kykx在第一象限内的图象与BC 边交于点D( 4,m),与AB 边交于点 E(2, n),△ BDE 的面积为 2.(1)求 m 与 n 的数量关系;(2)当 tan∠ A= 12时,求反比例函数的解析式和直线AB 的表达式;(3)设直线 AB 与 y 轴交于点 F,点 P 在射线 FD 上,在( 2)的条件下,如果△AEO 与△ EFP 相似,求点P 的坐标.图 1 学习必备欢迎下载例 5 如图 1,已知梯形OABC ,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出...