光学谐振腔的几何理论VIP免费

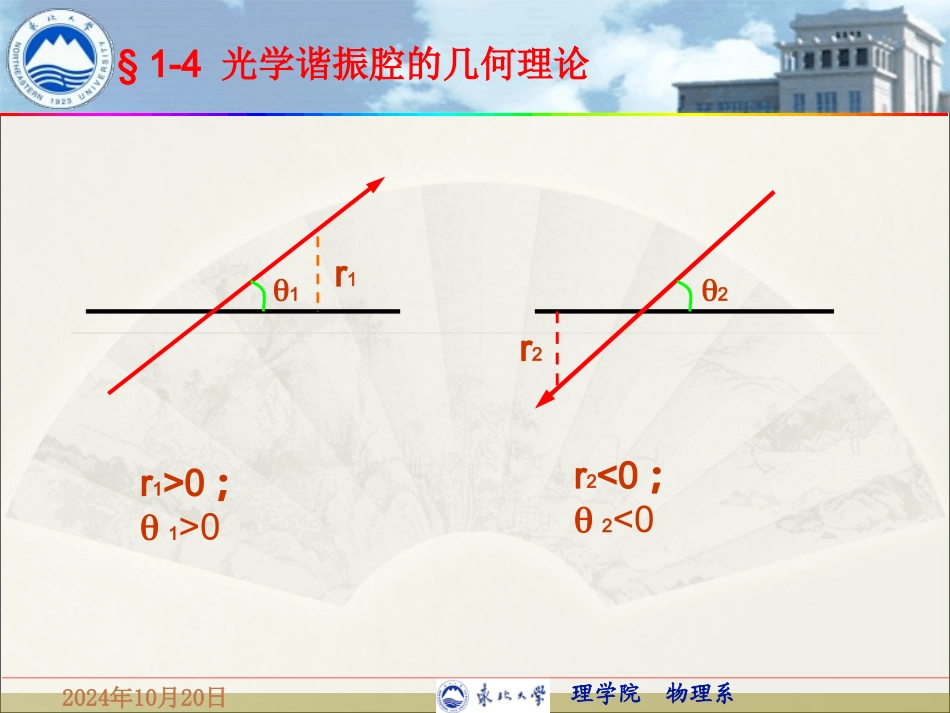
理学院物理系§1-4光学谐振腔的几何理论2024年10月20日一.光线在谐振腔内行为——光学变换矩阵光学变换矩阵：用矩阵表达方式，描述近轴光线经光学器件后传播特征的参数变化。近轴光线表征参数：光线离轴线距离r符号规则：光线与轴线夹角r正负光线在轴线上方取正光线在轴线下方取负正负光线出射方向在轴线上方取正光线出射方向在轴线下方取负理学院物理系§1-4光学谐振腔的几何理论2024年10月20日r11r22r1>0；1>0r2<0；2<0理学院物理系§1-4光学谐振腔的几何理论2024年10月20日rθ2121rrTABTCD：光线在某截面处的坐标向量T为光学变换矩阵，可表示为：理学院物理系§1-4光学谐振腔的几何理论2024年10月20日1.自由空间传播距离L12112tgLrr11tg21121rrL1122101rLrzθ1θ2Lr1r2近轴光线：理学院物理系§1-4光学谐振腔的几何理论2024年10月20日自由空间传播距离L，光学变化矩阵：101LT·Ar1(r2)BxOθ2θ1αβ2.球面反射镜光学变换矩阵O点：曲率中心，OA=R(曲率半径）α：入（反）射角入射（r1,θ1)β:AB圆心角反射（r2,θ2)理学院物理系§1-4光学谐振腔的几何理论2024年10月20日则：212112rr1rR1201RT212112rrrR近轴时，上述方程简化为：理学院物理系§1-4光学谐振腔的几何理论2024年10月20日讨论：①R=∞时，凹面平面②R取负值，凹面平面3.共轴球面谐振腔（往返一周）M2反射：M1反射1001T1201RT11,r22,r33,r55,r44,rM1M211,r22,r33,r44,r55,rLM1出发：自由T3自由T2凹反T4凹反理学院物理系§1-4光学谐振腔的几何理论2024年10月20日M1到M2:自由空间传播，故M2点反射：球面反射，M2到M1:自由空间传播21121110101rrLLT322322210102211rrTRR34334110101rrLLT理学院物理系§1-4光学谐振腔的几何理论2024年10月20日M1点反射：球面反射总光学变换矩阵T：整理，544541110102211rrTRR4321ABTTTTTCD221RLA221LBLR12124112LCRRRR12122211LLLDRRR理学院物理系§1-4光学谐振腔的几何理论2024年10月20日二.光学谐振腔稳定条件㈠稳定性条件：光线在腔内往返n次，nnnnnABTCDsinnsin1sin1sinsinsinsin(1)1arccos()2nAnBnTCnDnnAD理学院物理系§1-4光学谐振腔的几何理论2024年10月20日⑴若为虚数sin(n),sin(n-1)随n增大而呈指数增加，故An，Bn，Cn，Dn随n增大而增大，不能保证有限性，非稳腔;⑵若为实数.0或，sin(n),sin(n-1)在-1与1间，故矩阵无振荡变化，满足有限性，稳定腔;.=0或矩阵元为不定式，形成临界腔;故：为虚数：非稳腔为实数，且0或：稳定腔;=0或：临界腔;理学院物理系§1-4光学谐振腔的几何理论2024年10月20日又稳定腔临界腔非稳腔即：共轴球面腔的稳定条件：11()12AD1()112AD或1()112AD或1arccos()2AD1)(211DA理学院物理系§1-4光学谐振腔的几何理论2024年10月20日221LAR121222(1)(1)LLLDRRR2121112222()11122LLLLADRRRR122111LLRR代入上式，整理得12121,1LLggRR为腔结构（几何参数）理学院物理系§1-4光学谐振腔的几何理论2024年10月20日则稳定性条件可写为：1201gg0g12121...