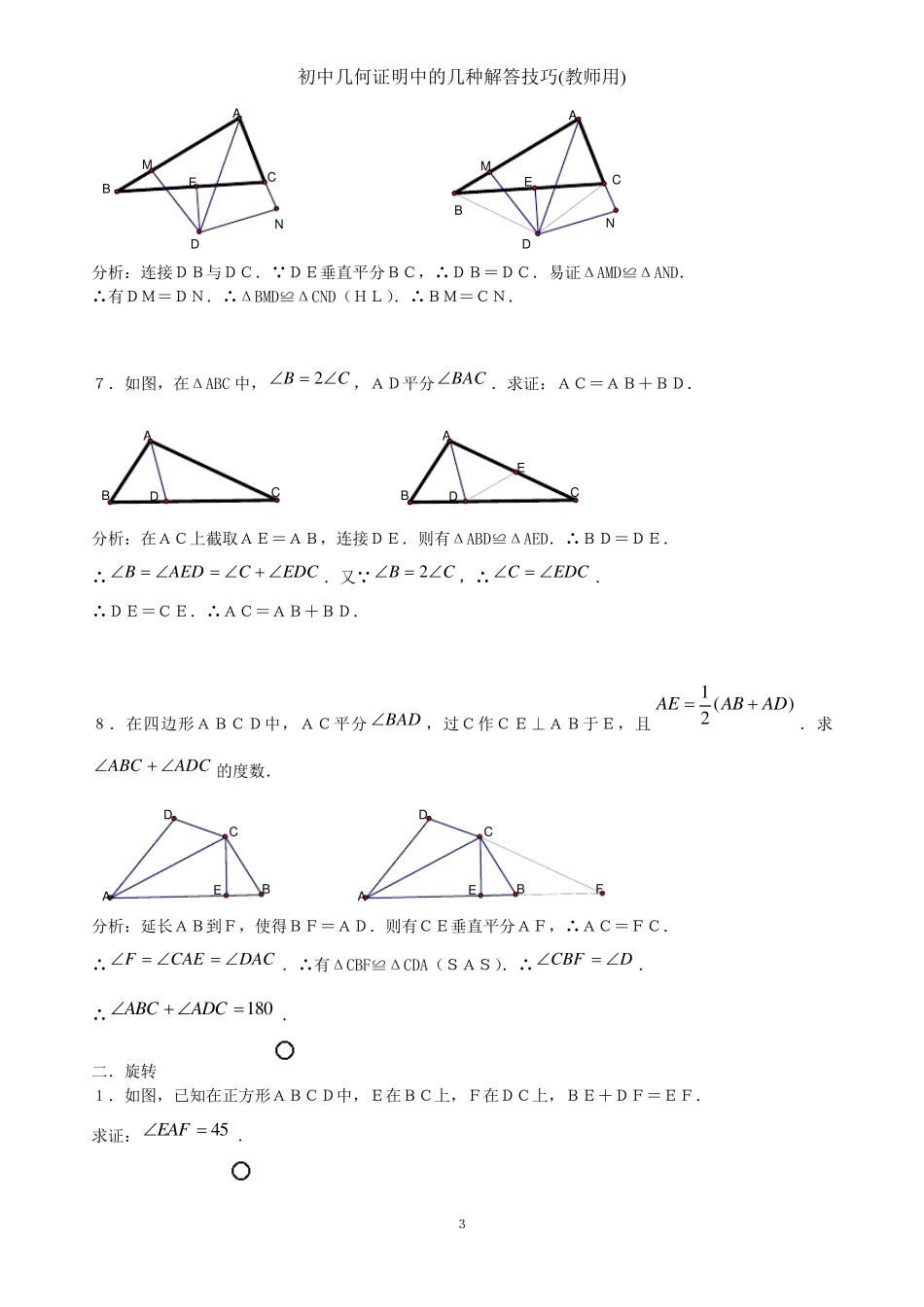
初中几何证明中的几种解答技巧(教师用) 1 几何证明中的几种技巧 一.角平分线--轴对称 1.已知在ΔABC 中,E为BC的中点,AD平分BAC,BDAD于D.AB=9,AC=13.求DE的长. CBADE CBADEF 分析:延长BD交AC于F.可得ΔABD≌ΔAFD.则BD=DF.又BE=EC,即DE为ΔBCF 的中位线.∴11 ()222DEFCACAB. 2.已知在ΔABC 中,108A ,AB=AC,BD平分ABC.求证:BC=AB+CD. DABC DABCE 分析:在BC上截取BE=BA,连接DE.可得ΔBAD≌ΔBED.由已知可得:18ABDDBE ,108ABED ,36CABC . ∴72DECEDC ,∴CD=CE,∴BC=AB+CD. 3.已知在ΔABC 中,100A ,AB=AC,BD平分ABC.求证:BC=BD+AD. ABCD ABCDEF 分析:在BC上分别截取BE=BA,BF=BD.易证ΔABD≌ΔEBD.∴AD=ED, 100ABED .由已知可得:40C,20DBF.由 BF=BD, ∴80BFD.由三角形外角性质可得:40CDFC .∴CF=DF. 100BED,∴80BFDDEF ,∴ED=FD=CF,∴AD=CF, 初中几何证明中的几种解答技巧(教师用) 2 ∴BC=BD+AD. 4.已知在ΔABC 中, ACBC,CEAB,AF平分CAB,过F作FD∥BC ,交AB于D.求 证:AC=AD. ACBEFD ACBEFDG 分析:延长DF交AC于G. FD∥BC,BC⊥AC,∴FG⊥AC. 易证ΔAGF≌ΔAEF.∴EF=FG.则易证ΔGFC≌ΔEFD.∴GC=ED. ∴AC=AD. 5.如图(1)所示,BD和CE分别是ABC 的外角平分线,过点A作AF⊥BD于F,AG⊥CE于G,延长AF及AG与BC相交,连接FG. (1)求证:1 ()2FGABBCCA (2)若(a)BD与CE分别是 ABC 的内角平分线(如图(2)); (b)BD是ΔABC 的内角平分线,CE是ΔABC 的外角平分线(如图(3)). 则在图(2)与图(3)两种情况下,线段FG与ΔABC 的三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明. GFABCEDHIFGABCDEIHGFABCDEIH 图(1) 图(2) 图(3) 分析:图(1)中易证ΔABF≌ΔIBF 及ΔACG≌ΔHCG.∴有AB=BI,AC=CH及AD=ID,AG=GH.∴GF为ΔAIH 的中位线.∴1 ()2FGABBCCA. 同理可得图...