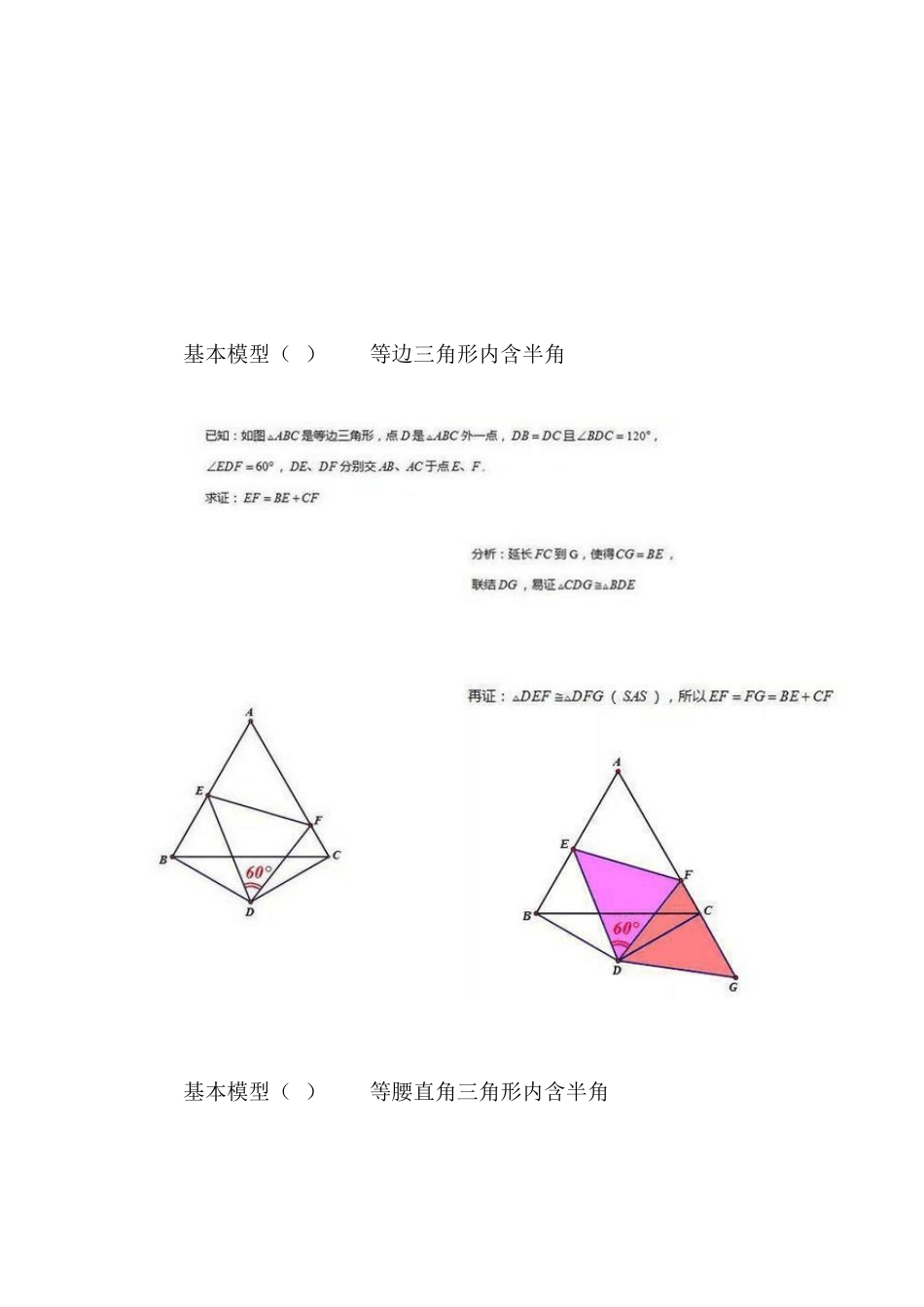
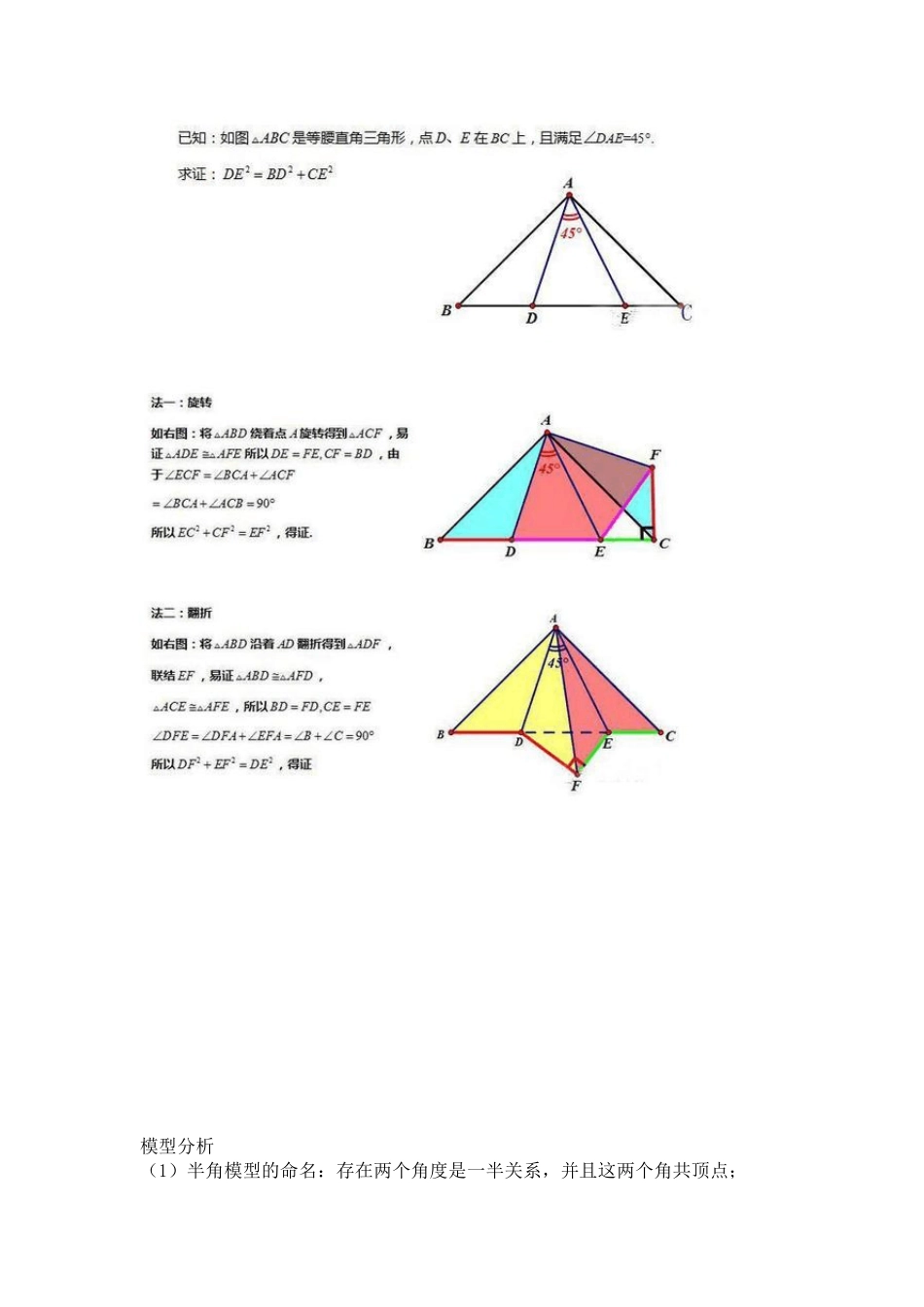
半角模型模型倍长中线或类中线(与中点有关的线段)构造全等三角形已知如图:∠2=12∠AOB,OA=OB。连接 FB,将△FOB绕点 O旋转至△F′OA的位置,连接 F′E、FE,可得△OEF′≌△OEF。基本模型(1)——正方形内含半角如图,在正方形 ABCD中,E、F分别是 BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。基本模型(2)——等边三角形内含半角基本模型(3)——等腰直角三角形内含半角模型分析(1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点;(2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系;(3)常见的半角模型是90°含 45°,120°含 60°。核心母题 如图,在正方形 ABCD 中,E、F 分别是BC、CD 边上的点,∠EAF=45°,求证:EF=BE+DF.变式一:如图,E、F 分别是边长为1 的正方形ABCD 的边BC、CD 上的点,若△ECF 的周长是2,求∠EAF 的度数?变式二:如图,在正方形ABCD 中,E、F 分别是BC、CD 边上的点,∠EAF=45°,AG⊥EF,求证:AG=AB.综合:在正方形ABCD 中,若M、N 分别在边BC、CD 上移动,且满足MN=BM+DN,求证:①.∠MAN=45②.ABCCMN2③.AM、AN分别平分∠BMN和∠DNM.练习1、如图,在四边形ABCD 中,AB=BC,∠A=∠C=90°,∠B=135°,K、N 分别是 AB、BC 上的点,若△BKN 的周长是 AB 的 2 倍,求∠KDN 的度数?2、已知:正方形ABCD 中,∠MAN=45°,∠MAN 绕点 A 顺时针旋转,它的两边分别交 CB、DC(或它们的延长线)于点 M、N.当∠MAN 绕点 A旋转到 BM=DN 时(如图1),易证 BM+DN=MN.(1)当∠MAN 绕点 A 旋转到 BM≠DN 时(如图2),线段 BM、DN 和 MN之间有怎样的数量关系?写出猜想,并加以证明;(2)当∠MAN 绕点 A 旋转到如图3的位置时,线段 BM、DN 和 MN 之间又有怎样的数量关系?请直接写出你的猜想.3、如图,在四边形ABCD 中,AB=AD,,∠B+∠D=180°,E、F 分别是边BC、CD 上的点,且 2∠EAF=∠BAD,(1)求证:EF=BE+FD(2)如果 E、F 分别是边BC、CD 延长线上的点,其他条件不变,结论是否仍然成立?说明理由。4、如图所示,在五边形ABCDE 中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°求证:AD 平分∠CDE.5、如图,已知 AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边形ABCDE的面积.6、如图1.在四边形ABCD 中.AB=AD,∠B+∠D=180 ゜,E、F 分别是边BC、CD 上的点,且∠BAD=2∠EAF.(1)求证:EF=BE+DF...