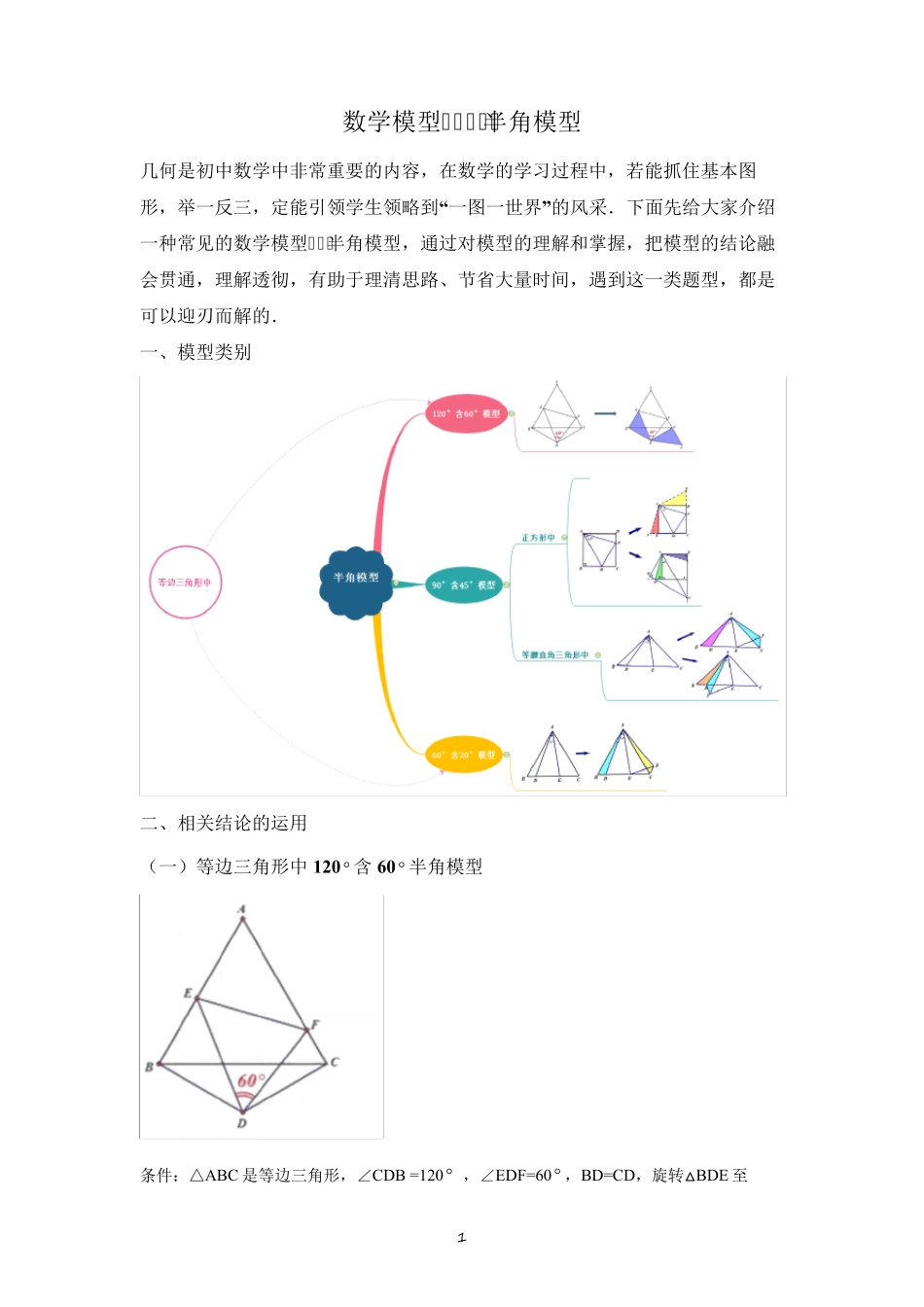
1 数学模型-----半角模型 几何是初中数学中非常重要的内容,在数学的学习过程中,若能抓住基本图形,举一反三,定能引领学生领略到“一图一世界”的风采.下面先给大家介绍一种常见的数学模型---半角模型,通过对模型的理解和掌握,把模型的结论融会贯通,理解透彻,有助于理清思路、节省大量时间,遇到这一类题型,都是可以迎刃而解的. 一、模型类别 二、相关结论的运用 (一)等边三角形中120 含60 半角模型 条件:△ABC 是等边三角形,∠CDB =120 ,∠EDF=60 ,BD=CD,旋转△BDE 至 2 △CDG 结论1:△FDE △FDG 结论2:EF=BE+CF 结论3: ∠DEB =∠DEF 典例精讲: 已知四边形 ABCD 中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN 绕 B 点旋转,它的两边分别交 AD,DC(或它们的延长线)于 E、F. (1)当∠MBN 绕 B 点旋转到 AE=CF 时(如图 1),试猜想 AE,CF,EF 之间存在怎样的数量关系?请将三条线段分别填入后面横线中: + = .(不需证明) (2)当∠MBN 绕 B 点旋转到 AE≠CF(如图 2)时,上述(1)中结论是否成立?请说明理由. (3)当∠MBN 绕 B 点旋转到 AE≠CF(如图 3)时,上述(1)中结论是否成立?若不成立,线段 AE,CF,EF 又有怎样的数量关系?请直接写出你的猜想,不需证明. 【思路点拨】 (1)证明△ABE≌△CBF 且△BEF 是等边三角形即可; (2)根据“半角”模型 1,先证△BAE≌△BCG,再根据“半角”模型 1 中的结论2 得出△GBF≌△EBF,再根据“半角”模型 1 中的结论3 即可; (3)根据“半角”模型 1,先证△BAH≌△BCF,再根据“手拉手”模型 1 中的结论2 得出△EBF≌△EBH 即可. 【详解】 解:(1)如图 1, 3 △ABE 和△CBF 中, AECFBAEBCFABCB , ∴△ABE≌△CBF(SAS), ∴∠CBF=∠EBA,BE=BF, ∠ABC=120°,∠EBF=60°, ∴△BEF 是等边三角形,CF= 12 B ,AE= 12 BE , ∴EF=BE=BF=AE+CF; (2)如图 2,延长 FC 至 G,使 AE=CG,连接 BG, 在△BAE 和△BCG 中, BABCBAEBCGAECG , ∴△BAE≌△BCG(SAS), ∴∠ABE=∠CBG,BE=BG, ∠ABC=120°,∠EBF=60°, ∴∠ABE+∠CBF=60°, ∴∠CBG+∠CBF=60°, ∴∠GBF=∠EBF, 在△GBF 和△EBF 中, BGBEG BFEBFBFBF ...