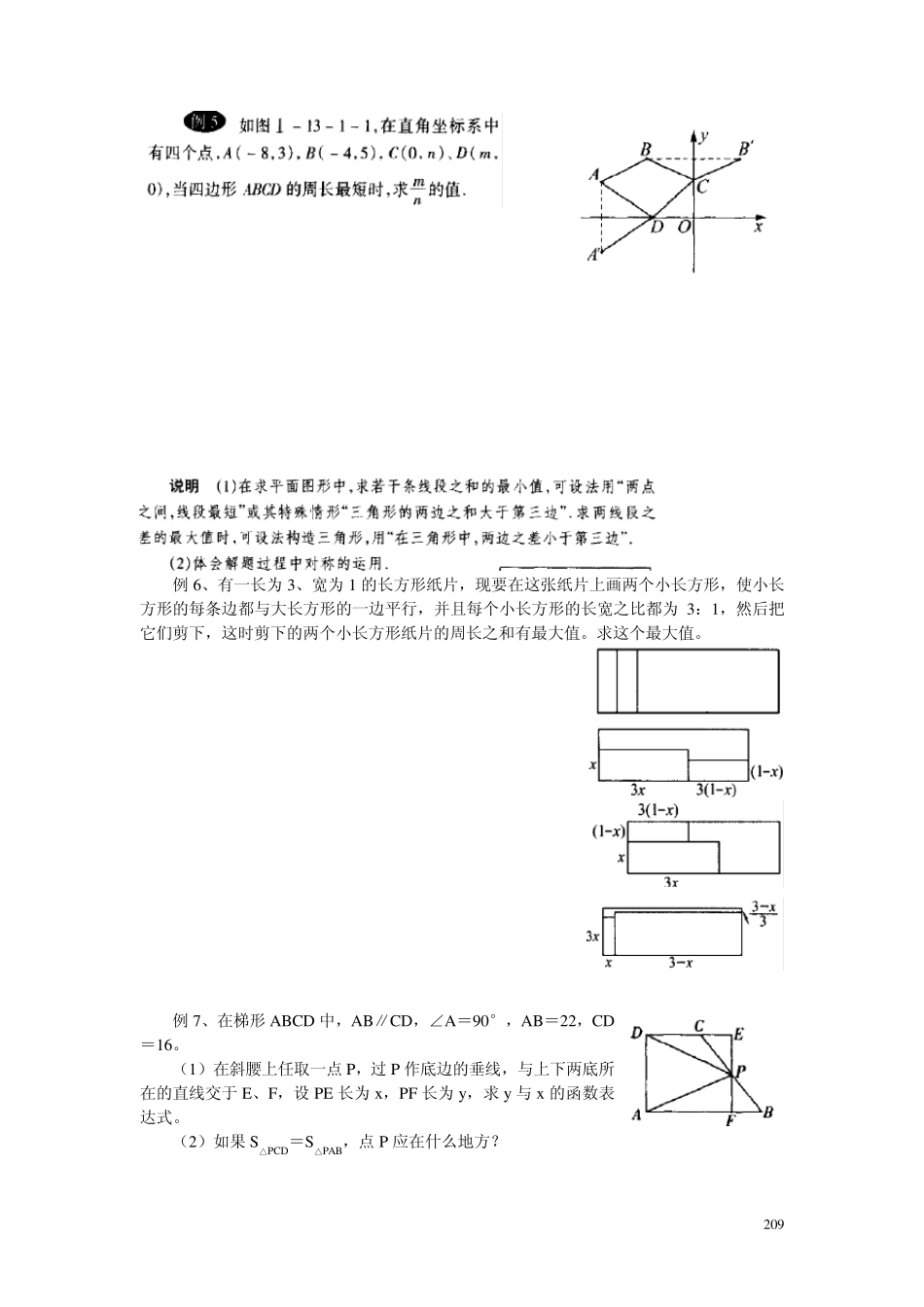
2 0 7 第十三章 函数图像与统计初步 第一节 正比例与反比例 【知识点拨】 (一)定义 1、函数y=kx+b,①k≠0时,称之为一次函数;k=0时,称之为常数函数。②b=0时称之为正比例函数。 (二)函数的性质 1、自变量的取值范围(非实际问题一般是使函数解析式有意义的一切实数,实际问题不要考虑实际意义) 2、函数值的范围 3、函数的图像 4、函数的单调性(是指函数值随自变量的变化而递增或递减的变化情况) 5、函数图像的对称性(是指中心对称、轴对称) 6、函数图像的特殊点(特别是图像与 x、y轴的交点、最高点、最低点、不动点等) (三)研究函数常见的问题 1、求函数的解析式 2、用函数的图像 3、研究与函数相关的性质 (四)思路与方法 一次函数(尤其是正比例函数)和反比例函数是比较简单同时又很重要的函数,有许多问题可以利用它们来研究,更重要的是研究它们的思想和方法也是研究其他的函数的思想和方法。 【赛题精选】 2 0 8 209 例6、有一长为3、宽为1 的长方形纸片,现要在这张纸片上画两个小长方形,使小长方形的每条边都与大长方形的一边平行,并且每个小长方形的长宽之比都为3:1,然后把它们剪下,这时剪下的两个小长方形纸片的周长之和有最大值。求这个最大值。 例7、在梯形ABCD 中,AB∥CD,∠A=90°,AB=22,CD=16。 (1)在斜腰上任取一点 P,过 P 作底边的垂线,与上下两底所在的直线交于 E、F,设 PE 长为x,PF 长为y,求y 与x 的函数表达式。 (2)如果 S△PCD=S△PAB,点 P 应在什么地方? 2 1 0 例8 、某家电生产企业跟踪市场调进分析,决定调整产品生产方案,准备每周(按 1 2 0个工时计算)生产空调器、彩电、冰箱共 3 6 0 台,且冰箱至少生产 6 0 台,已知生产这些家电产品每台所需工时和每台产值如下表: 家电名称 空调器 彩电 冰箱 工时 1 /2 1 /3 1 /4 产值(千元) 4 3 2 问每周生产空调、彩电、冰箱各多少台,才能使产值最高?最高产值是多少千元? 2 1 1 【针对训练】 2 1 2 2 1 3 第二节 图像解题 【知识点拨】 【赛题精选】 2 1 4 例2 、画函数21xxy的图像。 【说明】(1)解题步骤:先化函数解析式,再画图像,在画图像时要注意自变量x的范围。(2)本例可有如下变题。 变题 1、求函数21xxy的最小值。 变题 2、解不等式321xx。 215 例3、画出1 yx的图形,并求...