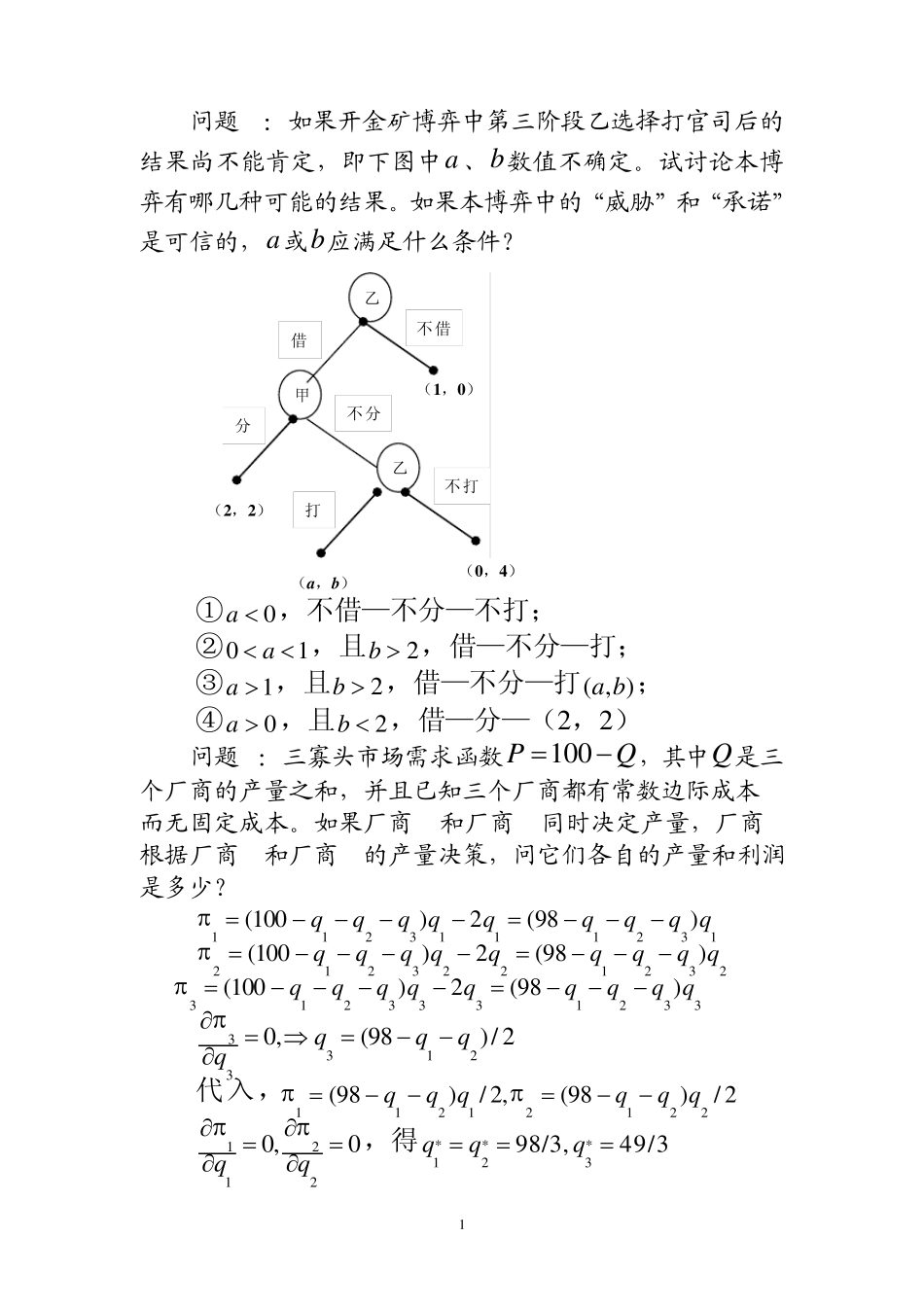
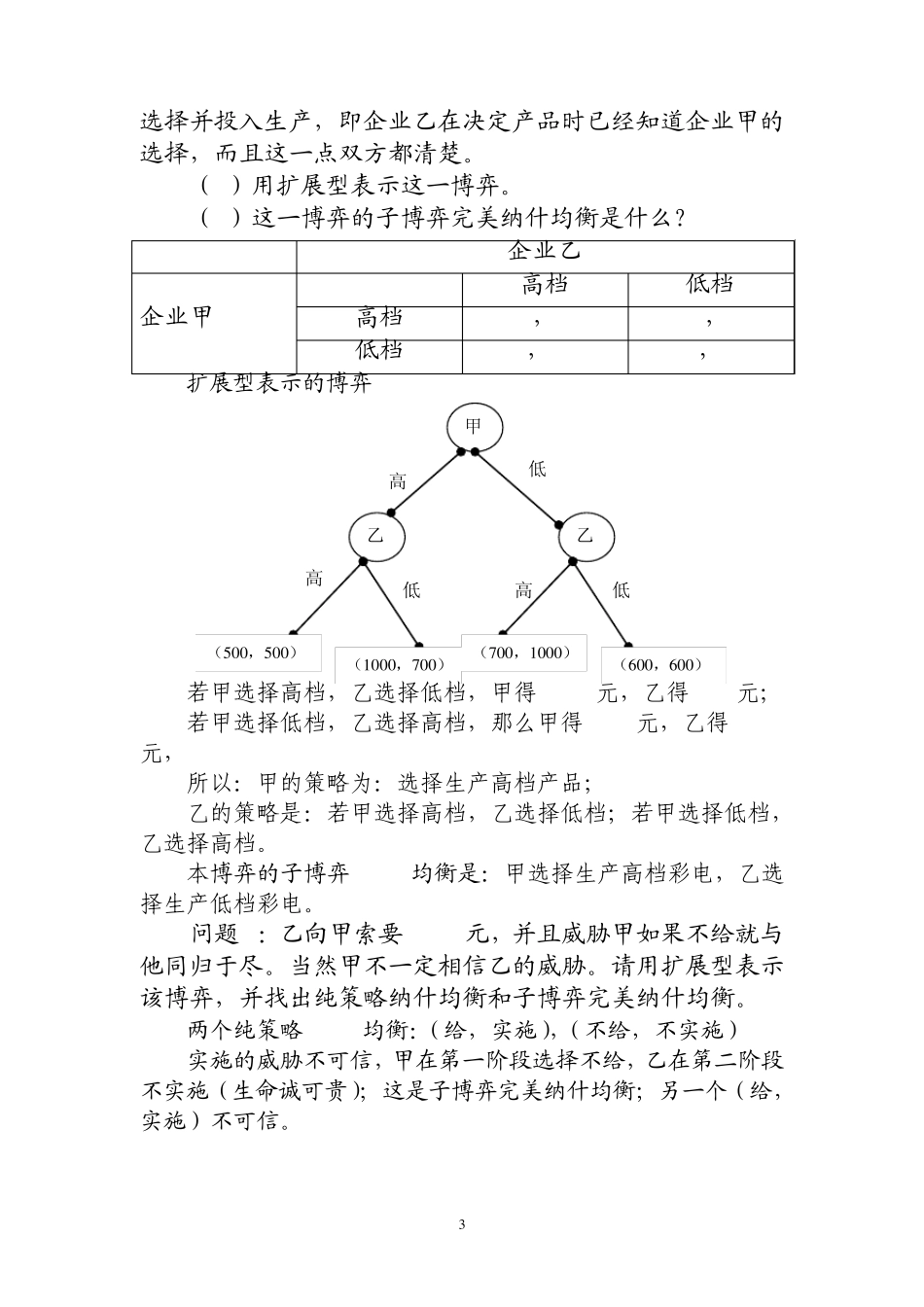
1 问题1:如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定,即下图中a、b数值不确定。试讨论本博弈有哪几种可能的结果。如果本博弈中的“威胁”和“承诺”是可信的,a或b应满足什么条件? ①0a ,不借—不分—不打; ②01a ,且2b ,借—不分—打; ③1a ,且2b ,借—不分—打( , )ab ; ④0a ,且2b ,借—分—(2 ,2 ) 问题2:三寡头市场需求函数QP1 0 0,其中Q是三个厂商的产量之和,并且已知三个厂商都有常数边际成本2而无固定成本。如果厂商 1和厂商 2同时决定产量,厂商 3根据厂商 1和厂商 2的产量决策,问它们各自的产量和利润是多少? 1123111231(1 0 0)2(9 8)qqq qqqqq q 2123221232(1 0 0)2(9 8)qqq qqqqq q 3123331233(1 0 0)2(9 8)qqq qqqqq q 331230 ,(9 8)/ 2qqqq 代入,11212122(9 8)/ 2 ,(9 8)/ 2qq qqq q 12120 ,0qq,得***1239 8 /3 ,4 9 /3qqq 乙 甲 乙 借 不借 分 不分 打 不打 (1 ,0 ) (2 ,2 ) (a,b) (0 ,4 ) 2 ***1234 8 0 2 /9 ,2 4 0 1 /9。 问题3:设两个博弈方之间的三阶段动态博弈如下图所示。 (1)若a和b分别等于 100和 150,该博弈的子博弈完美纳什均衡是什么? (2)TNL是否可能成为该博弈的子博弈完美纳什均衡路径,为什么? (3)在什么情况下博弈方2会获得 300单位或更高的得益? (1)博弈方1在第一阶段选择 R,在第三阶段选择 S,博弈方2在第二阶段选择 M。 (2)不可能。TNL带来的利益 50明显小于博弈方1在第一阶段R的得益 300;无论a和b是什么数值,该路径都不能构成 Nash均衡,不能成为子博弈完美 Nash均衡。 (3)由于TNL不是本博弈的子博弈完美 Nash均衡,因此博弈方2不可能通过该路径实现 300单位的得益,唯一有可能实现 300单位及以上的得益的路径为LNS,要使该路径成为子博弈完美 Nash均衡而且博弈方2得到 300单位及以上的得益必须3 0 0 ,3 0 0ab。 问题4:企业甲和企业乙都是彩电制造商,都可以选择生产低档产品或高档产品,每个企业在四种不同的情况下的利润如以下得益矩阵所示。如果企业甲先于企业乙进行产品1 2 1 L R M N S T 300,0 200,200 ...