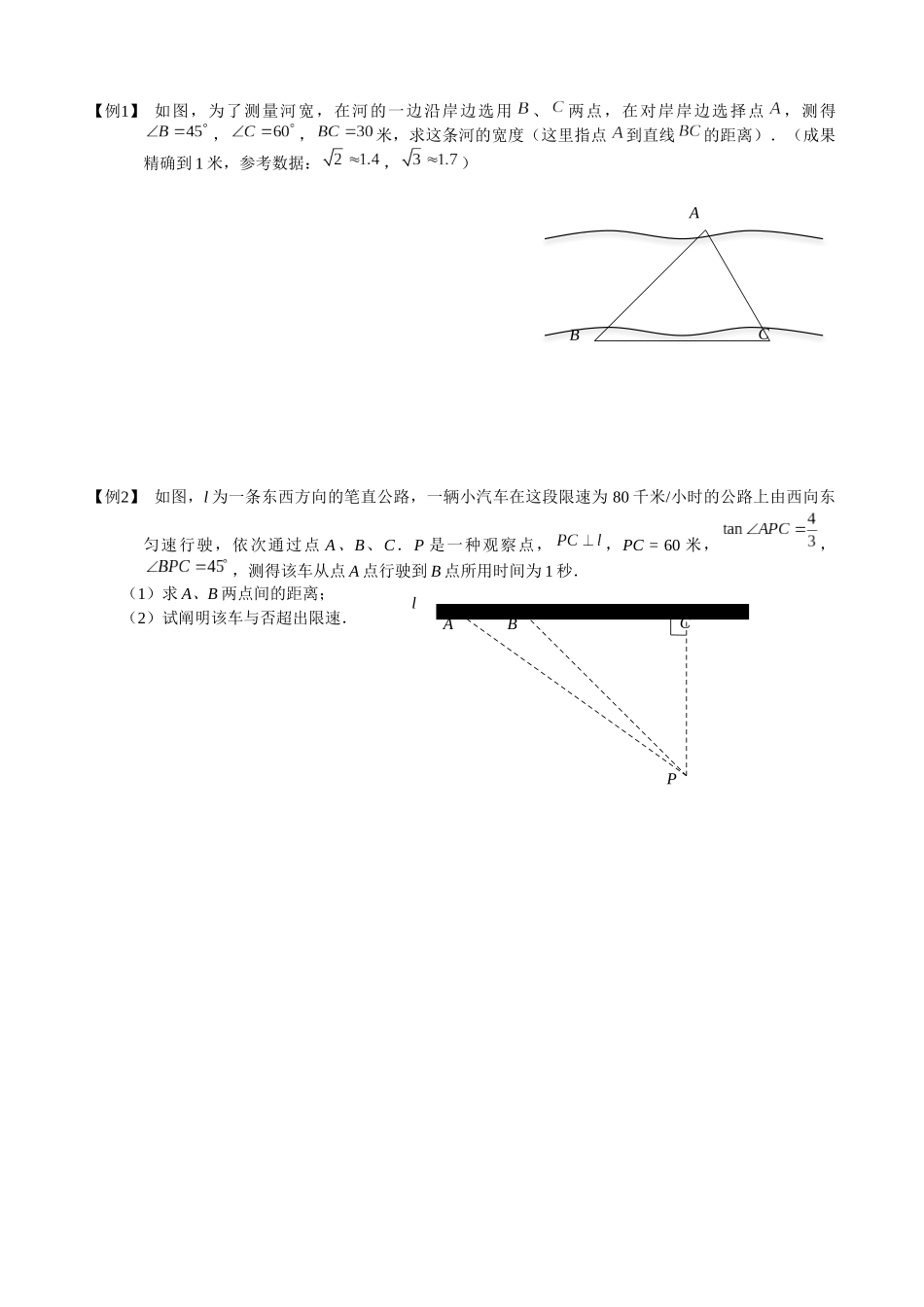
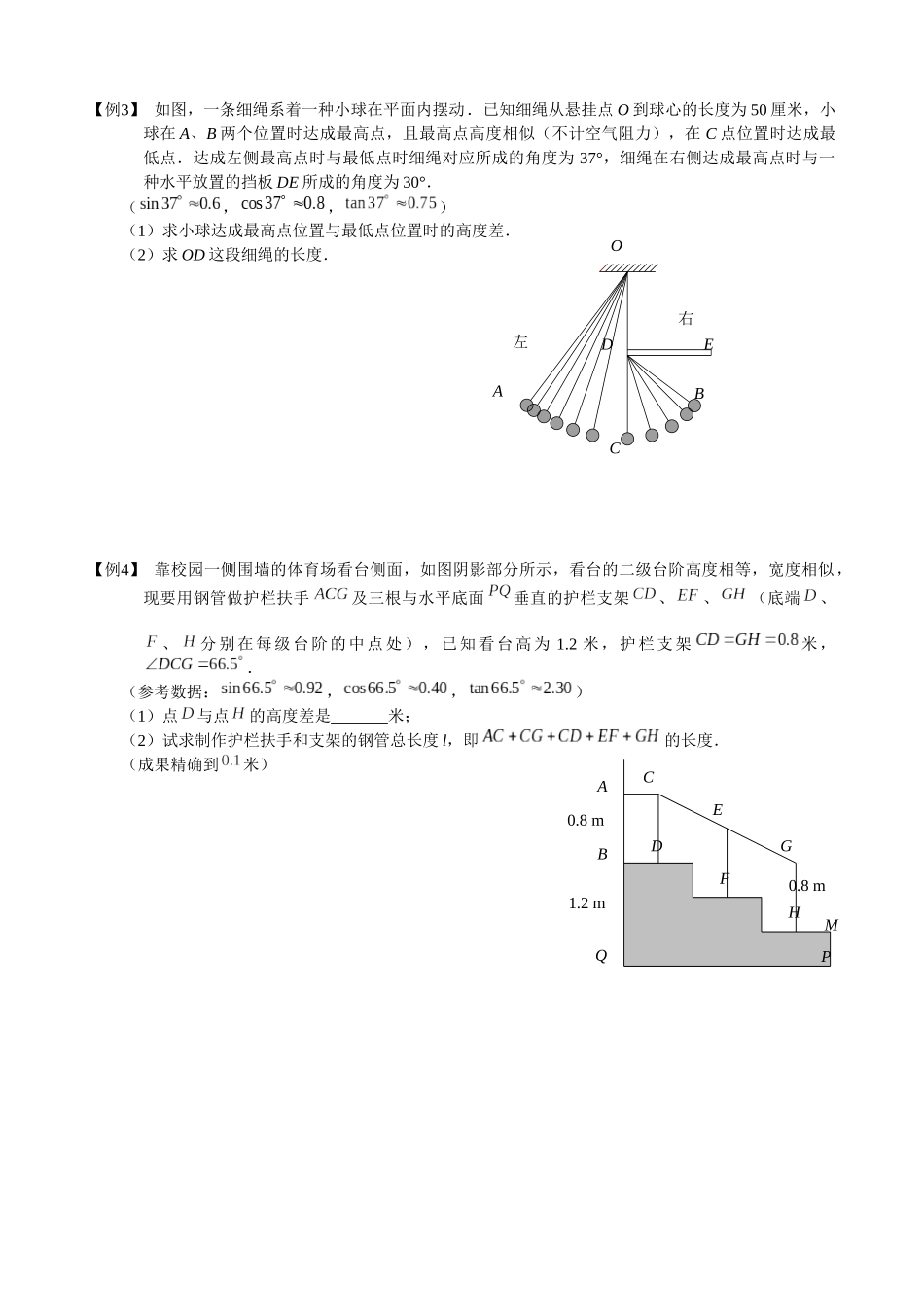
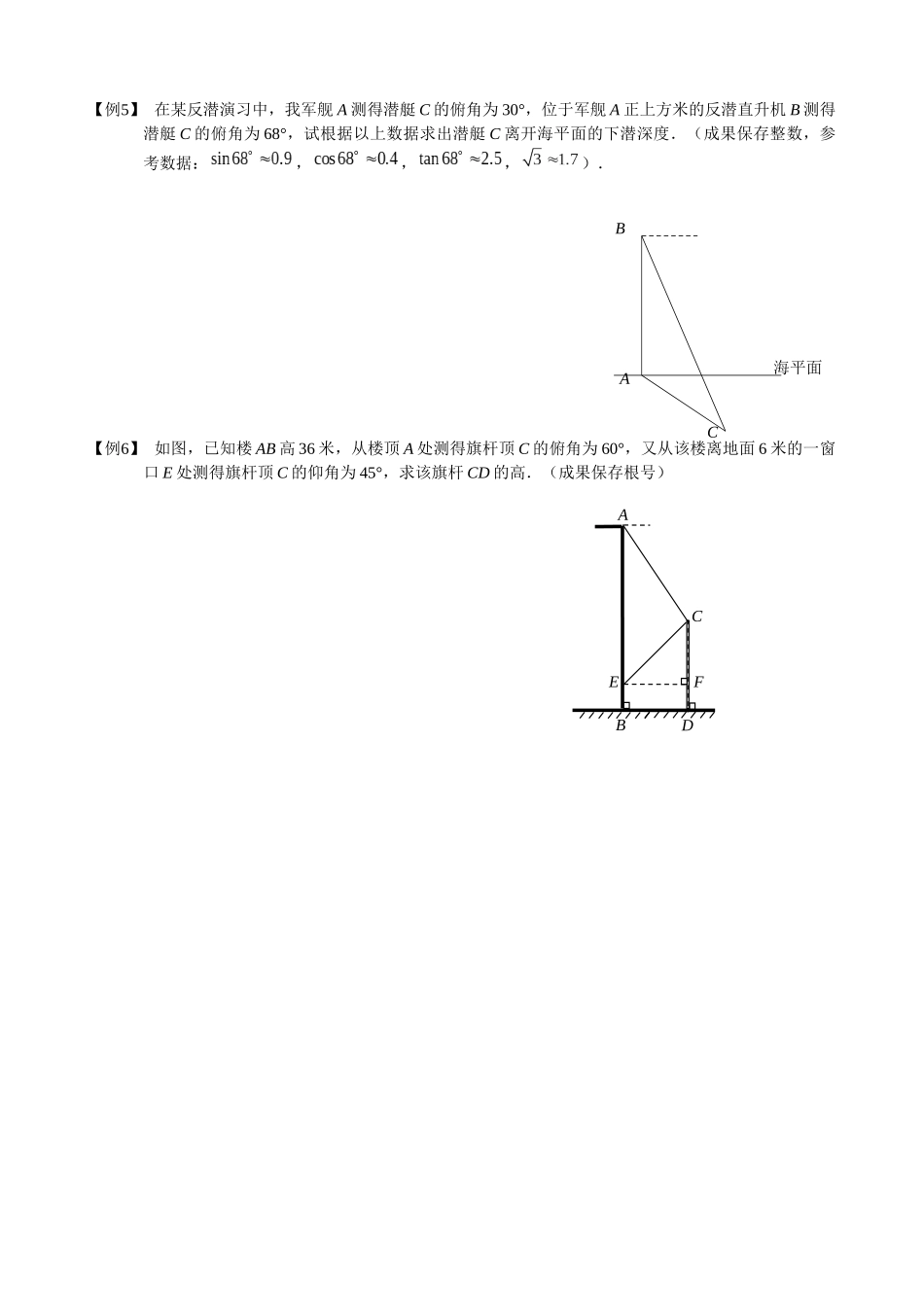
【例1】 如图,为了测量河宽,在河的一边沿岸边选用、两点,在对岸岸边选择点,测得,,米,求这条河的宽度(这里指点到直线的距离).(成果精确到 1 米,参考数据:,)【例2】 如图,l 为一条东西方向的笔直公路,一辆小汽车在这段限速为 80 千米/小时的公路上由西向东匀速行驶,依次通过点 A、B、C.P 是一种观察点,,PC = 60 米,,,测得该车从点 A 点行驶到 B 点所用时间为 1 秒.(1)求 A、B 两点间的距离;(2)试阐明该车与否超出限速.CBAlPCBA【例3】 如图,一条细绳系着一种小球在平面内摆动.已知细绳从悬挂点 O 到球心的长度为 50 厘米,小球在 A、B 两个位置时达成最高点,且最高点高度相似(不计空气阻力),在 C 点位置时达成最低点.达成左侧最高点时与最低点时细绳对应所成的角度为 37°,细绳在右侧达成最高点时与一种水平放置的挡板 DE 所成的角度为 30°.(,,)(1)求小球达成最高点位置与最低点位置时的高度差.(2)求 OD 这段细绳的长度.【例4】 靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的二级台阶高度相等,宽度相似,现要用钢管做护栏扶手及三根与水平底面垂直的护栏支架、、(底端、、分别在每级台阶的中点处),已知看台高为 1.2 米,护栏支架米,.(参考数据:,,)(1)点与点的高度差是 米;(2)试求制作护栏扶手和支架的钢管总长度 l,即的长度.(成果精确到米)右左OEDCBA0.8 m0.8 m1.2 mQPHGFEDCBAM【例5】 在某反潜演习中,我军舰 A 测得潜艇 C 的俯角为 30°,位于军舰 A 正上方米的反潜直升机 B 测得潜艇 C 的俯角为 68°,试根据以上数据求出潜艇 C 离开海平面的下潜深度.(成果保存整数,参考数据:,,,).【例6】 如图,已知楼 AB 高 36 米,从楼顶 A 处测得旗杆顶 C 的俯角为 60°,又从该楼离地面 6 米的一窗口 E 处测得旗杆顶 C 的仰角为 45°,求该旗杆 CD 的高.(成果保存根号)FECBDA海平面CBA【例7】 如图,从地面上的点 A 看一山坡上的电线杆 PQ,测得杆顶端点 P 的仰角是 26.6°,向前走 30 米达成 B 点,测得杆顶端点 P 和杆底端点 Q 的仰角分别是 45°和 33.7°.求该电线杆 PQ 的高度(成果精确到 1 米). (备用数据:,,,,,,,)【例8】 如图,小明想测量河对岸的一幢高楼 AB 的高度,小明在河边 C 处测得楼顶 A 的仰角是 60°.距C...