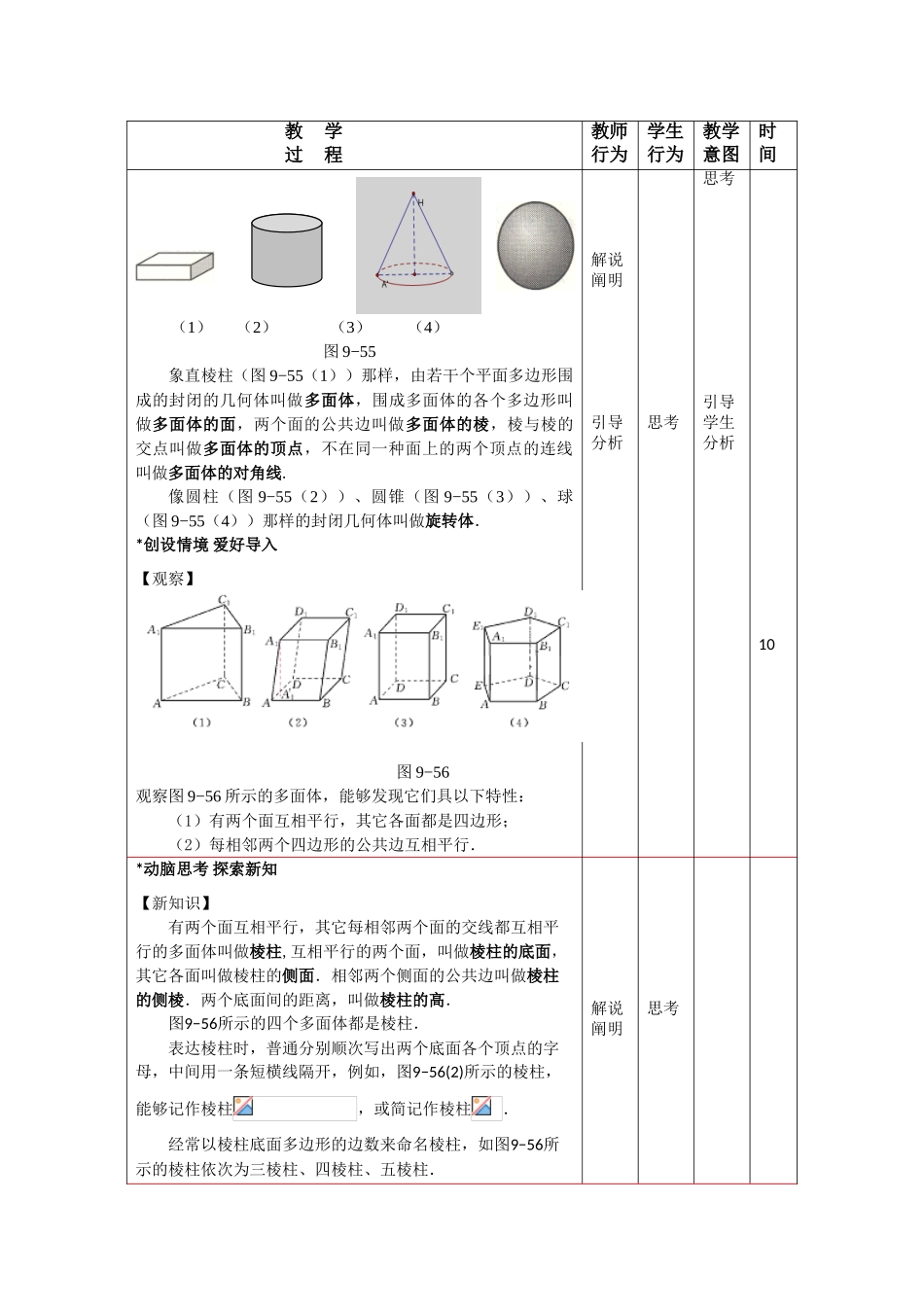
【课题】9.5 柱、锥、球及其简朴组合体(一)【教学目的】知识目的:(1)理解棱柱、棱锥的构造特性;(2)掌握棱柱、棱锥面积和体积计算.能力目的:培养学生的观察能力,数值计算能力及计算工具使用技能.【教学重点】正棱柱、正棱锥的构造特性及有关的计算.【教学难点】正棱柱、正棱锥的有关计算.【教学设计】教材首先介绍了多面体、旋转体的概念.然后通过观察模型,阐明棱柱、棱锥、圆柱、圆锥、球的构造特性及其面积、体积的计算公式.正棱柱的侧面积、全方面积、体积的计算公式经常使用,不要把侧面积、全方面积计算公式记混了.侧面都是全等的矩形的直四棱柱不一定是正四棱柱.底面是正方形的四棱柱不一定是正四棱柱.四棱锥 P-ABCD 中,如果棱锥的侧棱长相等,那么它一定是正四棱锥.如果棱锥的底面是正方形,那么它不一定是正四棱锥.例 1 是求正三棱柱的侧面积和体积的题目,例 2 是求正三棱锥的侧面积和体积的题目,要记住边长为 a 的正三角形的面积为.【教学备品】教学课件.【学时安排】2 学时.(90 分钟)【教学过程】教 学 过 程教师行为学生行为教学意图时间*揭示课题9.5 柱、锥、球及其简朴组合体【知识回想】在九年制义务教育阶段,我们学习过直棱柱、圆柱、圆锥、球等几何体.介绍质疑理解思考启发学 生0教 学 过 程教师行为学生行为教学意图时间(1) (2) (3) (4)图 9−55象直棱柱(图 9−55(1))那样,由若干个平面多边形围成的封闭的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的交点叫做多面体的顶点,不在同一种面上的两个顶点的连线叫做多面体的对角线.像圆柱(图 9−55(2))、圆锥(图 9−55(3))、球(图 9−55(4))那样的封闭几何体叫做旋转体.*创设情境 爱好导入【观察】 图 9−56观察图 9−56 所示的多面体,能够发现它们具以下特性:(1)有两个面互相平行,其它各面都是四边形;(2)每相邻两个四边形的公共边互相平行.解说阐明引导分析思考思考引导学生分析10*动脑思考 探索新知【新知识】有两个面互相平行,其它每相邻两个面的交线都互相平行的多面体叫做棱柱,互相平行的两个面,叫做棱柱的底面,其它各面叫做棱柱的侧面.相邻两个侧面的公共边叫做棱柱的侧棱.两个底面间的距离,叫做棱柱的高.图9−56所示的四个多面体都是棱柱.表达棱柱时,普通分别顺次写出两个底面各个顶点的字母,中间用一条短横线...