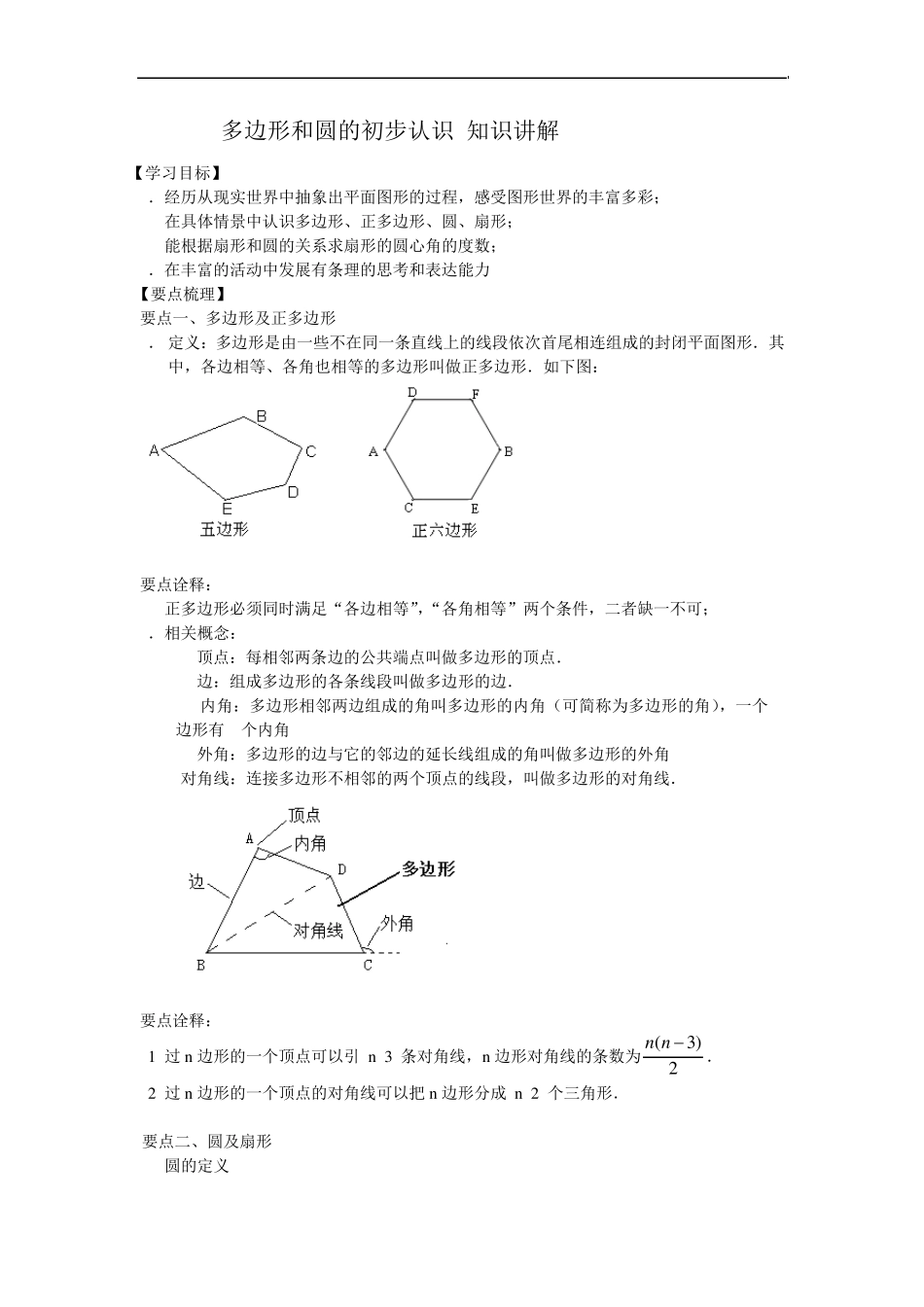
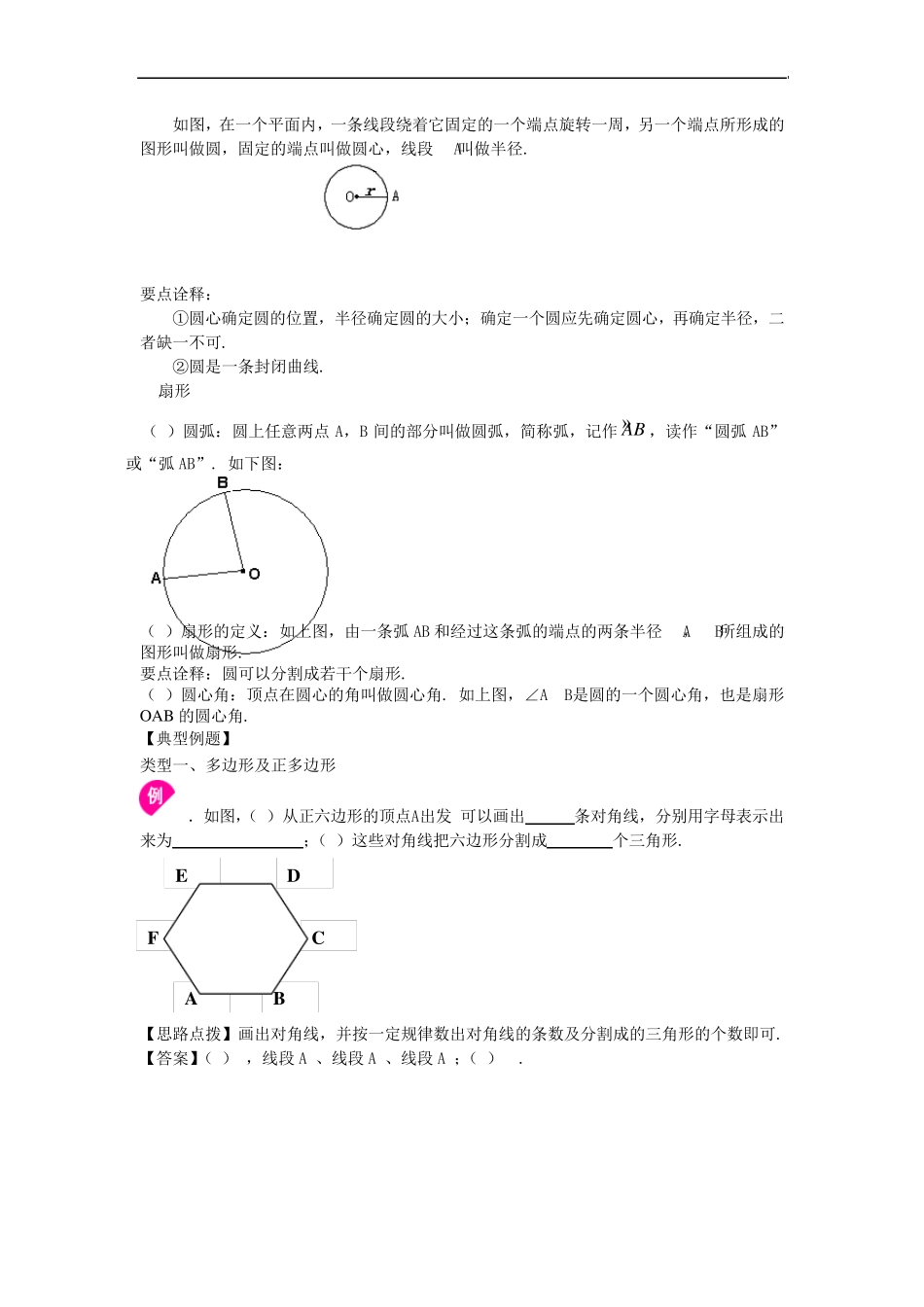
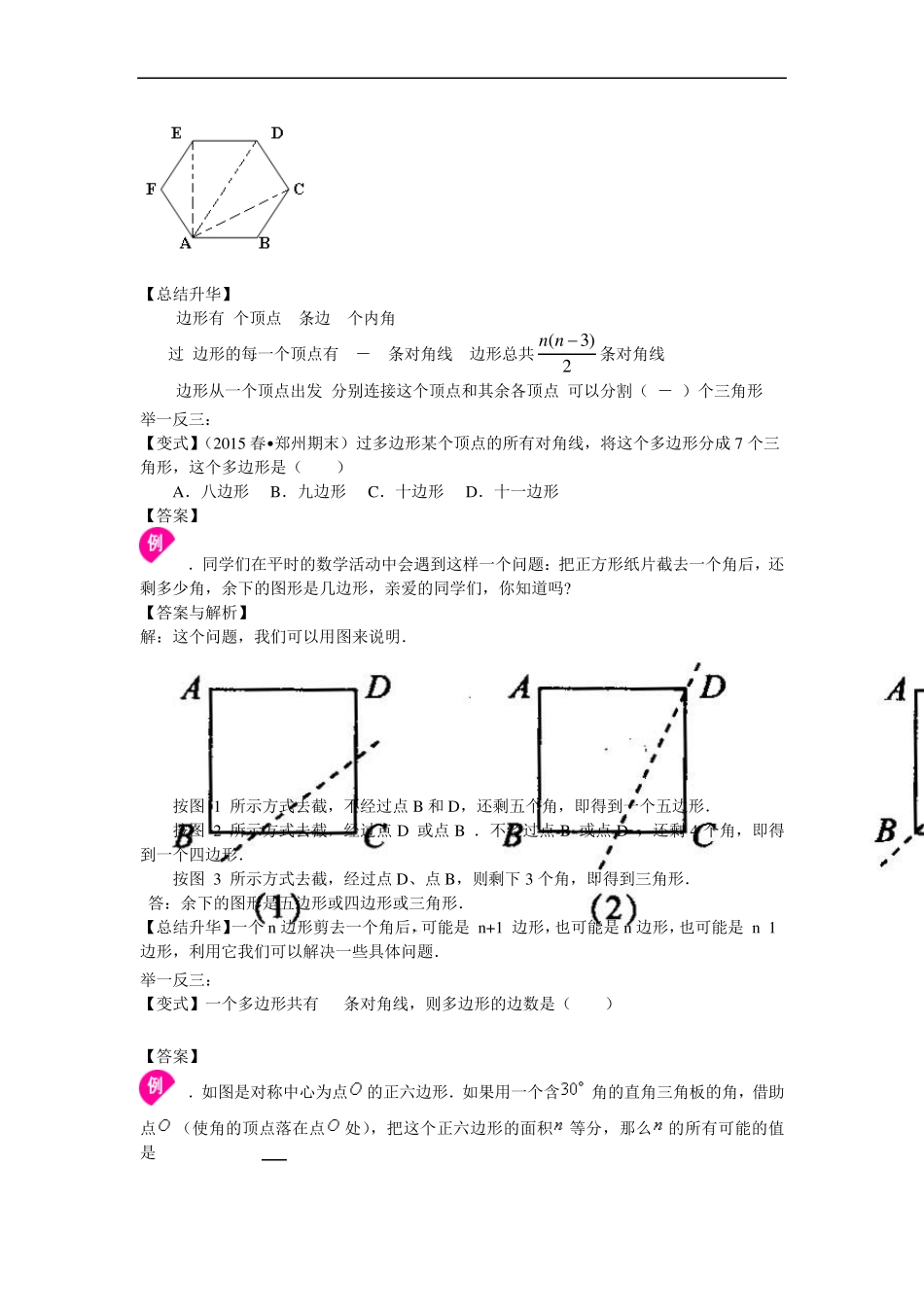
多边形和圆的初步认识 知识讲解 【学习目标】 1.经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩; 2. 在具体情景中认识多边形、正多边形、圆、扇形; 3. 能根据扇形和圆的关系求扇形的圆心角的度数; 4.在丰富的活动中发展有条理的思考和表达能力. 【要点梳理】 要点一、多边形及正多边形 1. 定义:多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形.其中,各边相等、各角也相等的多边形叫做正多边形.如下图: 要点诠释: 正多边形必须同时满足“各边相等”,“各角相等”两个条件,二者缺一不可; 2.相关概念: 顶点:每相邻两条边的公共端点叫做多边形的顶点. 边:组成多边形的各条线段叫做多边形的边. 内角:多边形相邻两边组成的角叫多边形的内角(可简称为多边形的角),一个 n边形有n个内角. 外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角. 对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 要点诠释: (1 )过n 边形的一个顶点可以引(n -3 )条对角线,n 边形对角线的条数为 (3)2n n . (2 )过n 边形的一个顶点的对角线可以把 n 边形分成(n -2 )个三角形. 要点二、圆及扇形 1. 圆的定义 如图,在一个平面内,一条线段绕着它固定的一个端点旋转一周,另一个端点所形成的图形叫做圆,固定的端点叫做圆心,线段OA叫做半径. 要点诠释: ①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可. ②圆是一条封闭曲线. 2.扇形 (1)圆弧:圆上任意两点A,B 间的部分叫做圆弧,简称弧,记作»AB ,读作“圆弧AB”或“弧AB”. 如下图: (2)扇形的定义:如上图,由一条弧AB 和经过这条弧的端点的两条半径OA,OB所组成的图形叫做扇形. 要点诠释:圆可以分割成若干个扇形. (3)圆心角:顶点在圆心的角叫做圆心角. 如上图,∠AOB是圆的一个圆心角,也是扇形OAB 的圆心角. 【典型例题】 类型一、多边形及正多边形 1.如图,(1)从正六边形的顶点A出发,可以画出 条对角线,分别用字母表示出来为 ;(2)这些对角线把六边形分割成 个三角形. 【思路点拨】画出对角线,并按一定规律数出对角线的条数及分割成的三角形的个数即可. 【答案】(1)3,线段AC、线段AD、线段AE;(2)4. E A B C F D 【总结升华】 (1) n边形有n个顶点,n条边,n个内角. (2) 过n边形...