大一高等数学期末考试试题VIP免费

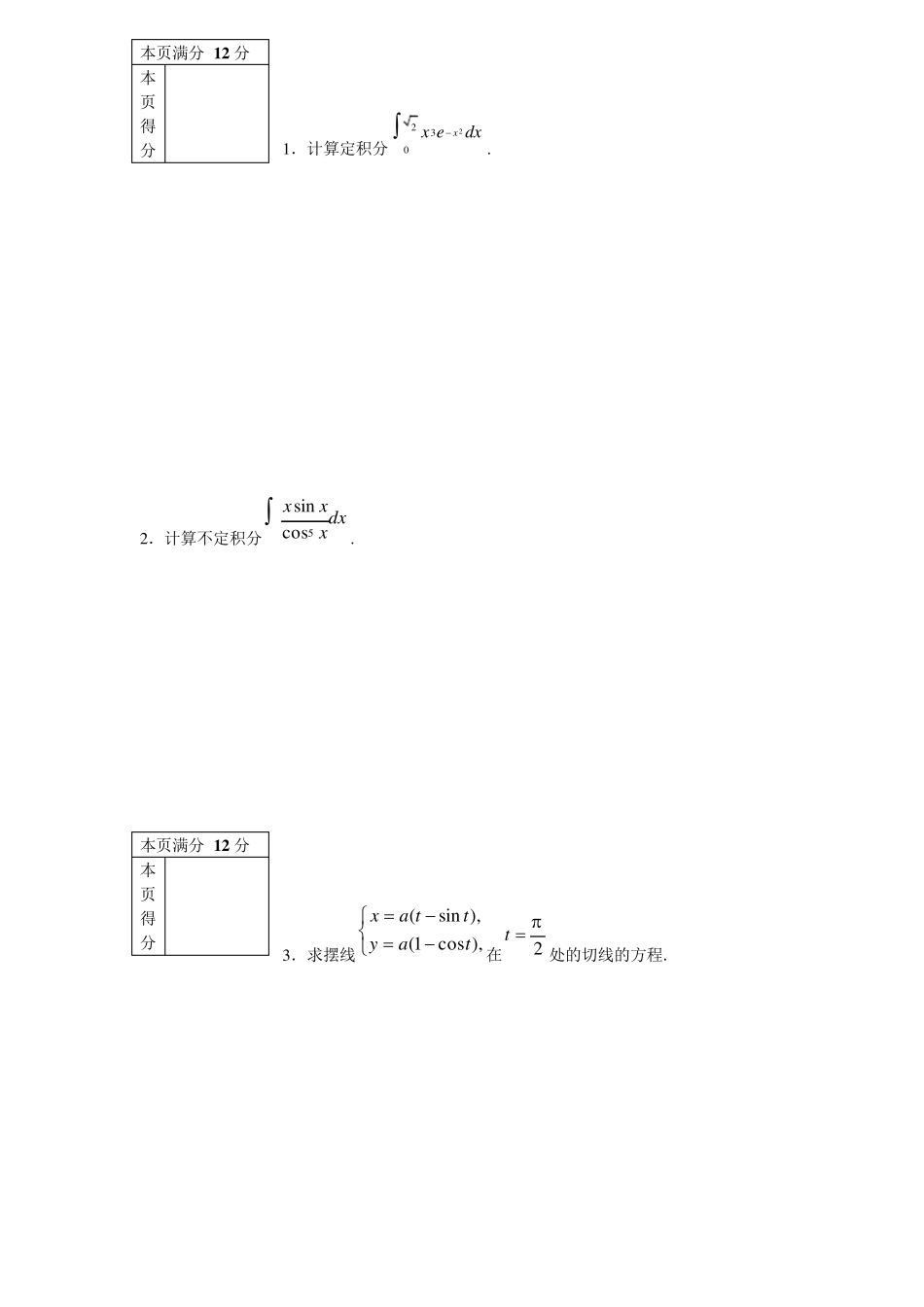
2012 学年第一学期 《高等数学（2-1）》期末模拟试卷 专业班级 姓 名 学 号 开课系室 高等数学 考试日期 2012 年12 月 11 日 页 号 一 二 三 四 五 六 总分 得 分 阅卷人 注 意 事 项 1．请在试卷正面答题，反面及附页可作草稿纸； 2．答题时请注意书写清楚，保持卷面清洁； 3．本试卷共五道大题，满分 100 分；试卷本请勿撕开，否则作废. 一．填空题（共 5 小题，每小题 4 分，共计 20 分） 1． . 2． . 3．设函数由方程确定，则 . 4. 设可导，且，，则 . 5．微分方程的通解为 . 二．选择题（共 4 小题，每小题 4 分，共计 16 分） 1．设常数，则函数在内零点的个数为（ ）. (A) 3 个; (B) 2 个; (C) 1 个; (D) 0 个. 2． 微分方程的特解形式为（ ）. （A）; （B）; （C）; （D）. 3．下列结论不一定成立的是（ ）. （A）若,则必有; （B）若在上可积,则; （C）若是周期为的连续函数,则对任意常数都有;（D）若可积函数为奇函数,则也为奇函数. 4. 设, 则是的（ ）. (A) 连续点; (B) 可去间断点; (C) 跳跃间断点; (D) 无穷间断点. 三．计算题（共 5 小题，每小题 6 分，共计 30 分） 210lim()xxxex1200511xxxxeedx( )yy x21xytedtx0xdydx  xf1( )( )x tf t dtf x1)0(f xf044yyy0kkexxxf ln)(),0(43cos2yyx cos2yAx cos2yAxx cos2sin 2yAxxBxx xAy2sin*  badc,,  badcdxxfdxxf0)(xfba, 0baf x dx  xfTa  TTaadxxfdxxf0 xf 0x t f t dt xxeexf113210x)(xf本页满分 3 6 分 本页得分 1．计算定积分. 2．计算不定积分. 3．求摆线在处的切线的方程. 2230xx edxdxxxx5cossin),cos1(),sin(tayttax2t本页满分 1 2 分 本页得分 本页满分 1 2 分 本页得分 4. 设，求. 5．设，求 . 四．应用题（共3 小题，每小题9 分，共计27 分） 1．求由曲线与该曲线过坐标原点的切线及轴所围图形的面积. 20( )cos()xF xxt dt)(xFnnnnnxnn)2()3)(2)(1(nnxlim2xyx本页满分1 5 分 本页得分 2．设平面图形由与所确定，试求绕直线 旋转一周...