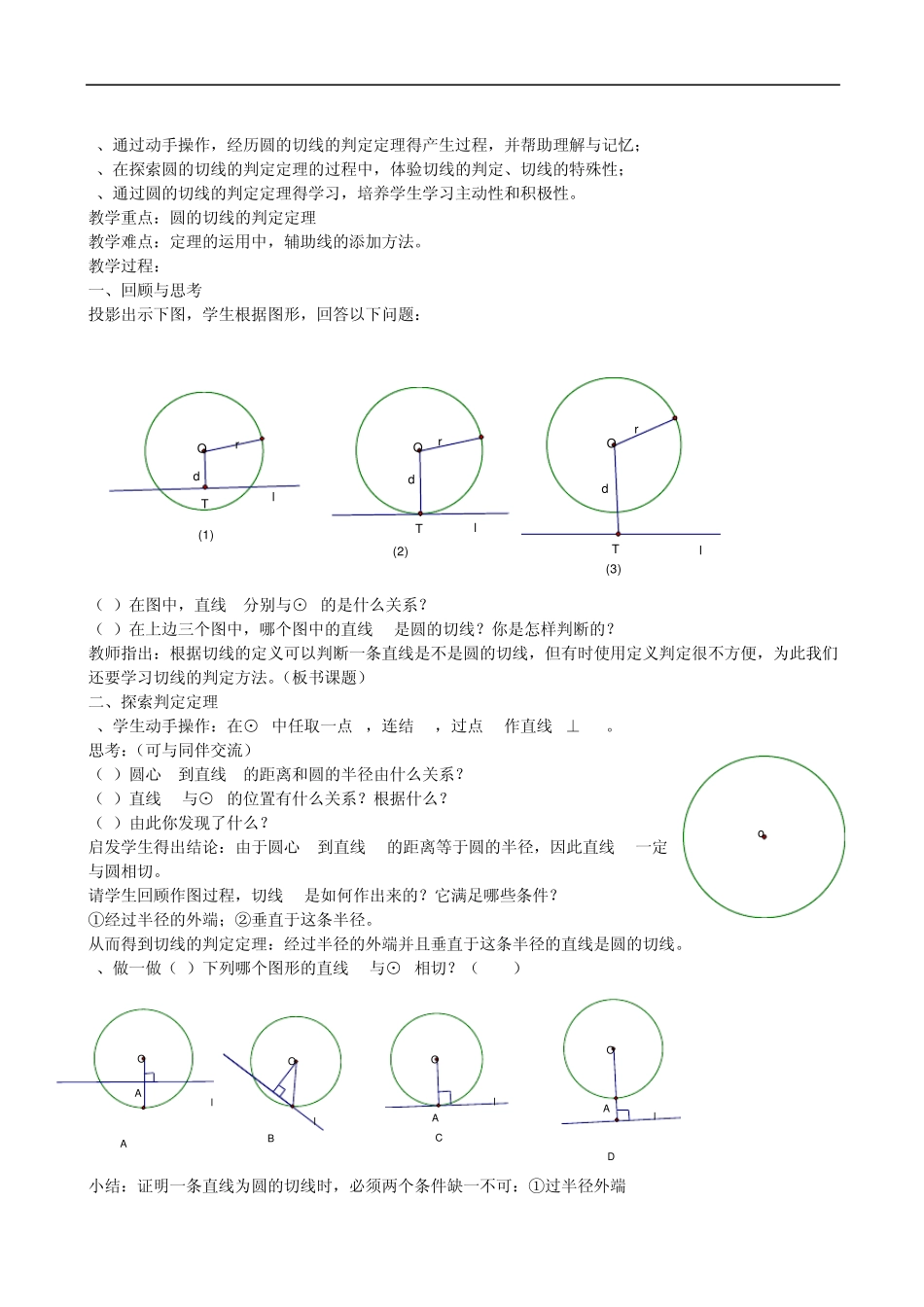
ldllrdrdr(3) (2) (1) OOTOTT九年级数学第三章直线与圆、圆与圆的位置关系全章教案 课题:3.1直线与圆的位置关系(1) 教学目标: 1、利用投影演示,动手操作探索直线和圆的运动变化过程,经历直线与圆的三种位置关系得产生过程; 2、在运动中体验直线与圆的位置关系,并观察理解直线与圆的“公共点的个数”的变化,培养猜想、分析、概括、归纳能力。 3、正确判别直线与圆的位置关系,或根据直线与圆的位置关系正确的得出圆心到直线的距离与圆的半径之间的大小关系或直线与圆的公共点的个数。 教学重点:直线与圆的三种位置关系 教学难点:直线与圆的三种位置关系的性质和判定俄正确运用 教学过程: 一、创设情景,引入新课 电脑演示:海上日出 1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的? 2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的? 你发现这个自然现象反映出直线和圆的位置关系有哪几种? 二、探究直线与圆的位置关系 1、动手操作:作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺, 仔细观察,直线和圆的交点个数如何变化? 在学生回答得基础上,教师指出:由直线和圆的公共点的个数,得出直线和圆的三种位置关系 : (1)相交:直线与圆有两个公共点时,叫做直线与圆相交,这时的直线叫做圆的割线; (2)相切:直线与圆有唯一公共点时,叫做直线与圆相切,这条直线叫做圆的切线,公共点叫做切点; (3)直线与圆没有公共点时,叫做直线与圆相离。 2、做一做: 如图,O为直线L外一点,OT⊥L,且 OT=d。请以 O为圆心,分别以 ddd23,,21 为半径画圆.所画的圆与直线l有什么位置关系? 3、直线与圆的位置关系量化 观察所画图形,你能从 d 和r 的关系发现直线l和圆O的位置关系吗? 学生回答后,教师总结并板书: 如果⊙O的半径 w为 r ,圆心 O 到直线 l的距离为 d,,那么: (1)直线l和⊙O相交 d<r; (2) 直线l和⊙O相切 d=r; TlO 4560HpAB(3)直线l和⊙O相离 d>r; 三、例题分析,课堂练习 例1、在Rt△ABC 中,∠C=90°,AC=3cm,BC=4cm,以 C 为圆心,r为半径的圆与 AB有怎样的位置关系?为什么? (1)r=2cm,(2)r=2.4cm,(3)r=3cm.(此题为课本第 49页课内练习第 1题的第 2小题) 分析:因为题中给出了⊙C的半径,所以解题的关键是求圆心到直线的距离,然后与 r 比较,确定⊙C与AB的关系。 练习:课本第 49页课内练习第 1题的第 1小题,...