力的分解习题VIP免费

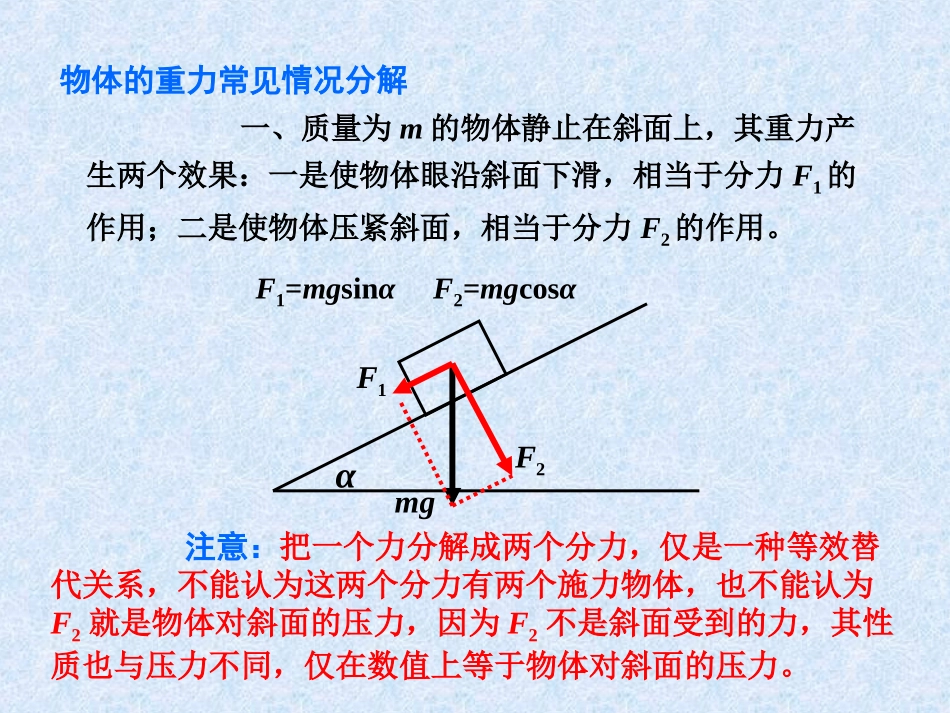
§3-5力的分解习题一、质量为m的物体静止在斜面上，其重力产生两个效果：一是使物体眼沿斜面下滑，相当于分力F1的作用；二是使物体压紧斜面，相当于分力F2的作用。F1=mgsinαF2=mgcosαmgF1F2α注意：把一个力分解成两个分力，仅是一种等效替代关系，不能认为这两个分力有两个施力物体，也不能认为F2就是物体对斜面的压力，因为F2不是斜面受到的力，其性质也与压力不同，仅在数值上等于物体对斜面的压力。物体的重力常见情况分解二、质量为m的光滑小球被竖直挡板档住而静止于斜面上时,其重力产生两个效果：一是使球压紧档板，相当于分力F1的作用；二是使球压紧斜面，相当于分力F2的作用:F1=mgtanαF1F2mgα物体的重力常见情况分解cos2mgF三、质量为m的光滑小球被悬线挂在竖直墙壁上,其重力产生两个效果:一是使球压紧竖直墙壁，相当于分力F1的作用；二是使球拉紧悬线，相当与分力F2的作用。F1=mgtanααF1F2mgα物体的重力常见情况分解cos2mgF四、A、B两点位于同一水平面上，质量为m的物体被AO、BO两根等长的细线拉住，其重力产生两个效果：一是拉紧AO线，相当于分力F1的作用；二是拉紧BO线，相当于分力F2的作用。F1=F2=mg/2sinα物体的重力常见情况分解αααF2F1mgABO五、质量为m的物体被支架悬挂而静止，其重力产生两个效果：一是拉伸AB，相当于分力F1的作用；二是压缩BC，相当于分力F2的作用。F1=mgtanαF2=mg/cosαααABCmgF1F2物体的重力常见情况分解力的分解问题的关键是根据力的作用效果，画出力的平行四边形，接着就转化为一个根据已知边角关系求解的几何问题。其基本程序可表示为：实际问题确定分力的方向物理抽象作出平行四边形数学计算求分力根据力的作用效果根据平行四边定则把对力的计算转化为边角的计算力的正交分解（1）力的正交分解法：把力沿着两个选定的互相垂直的方向分解，叫力的正交分解法。（2）正交分解的原理：一条直线上的两个或两个以上的力,其合力可由代数运算求得.当物体受到多个力作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便,为此建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴上,分别求出两个不同方向的合力Fx和Fy,然后可以由,求合力。22yxFFF例1：一个物体受到四个力的作用，已知F1=1N，方向正东；F2=2N，方向东偏北600，F3=N，方向西偏北300；F4=4N，方向东偏南600，求物体所受的合力。33F1F2F3F4xyF2xF2yF3yF3xF4xF4y600300600F1F2F3F4xyF2xF2yF3yF3xF4xF4y600300600yyyyFFFF432xxxxFFFFF4321)(2/122/331160cos430cos3360cos21000N)(2/33222/33360sin430sin3360sin2000N2/3Fy=NFx=-1/2NF=1NxyNFFFyx1)2/1()2/3(222232/12/3tanxyFF060例2.如图所示，悬挂物体的重力为G，杆重不计，绳子OA与杆OB的夹角为θ，求OA绳子和杆OB所受到的力。OABθGG1G2θ例3.如图所示，绳子MO与NO所能承受的最大拉力相同，长度MO>NO，则在不断增加重物G的重力过程中（绳OG不会被拉断）（）A、ON先被拉断B、OM先被拉断C、OM和ON同时被拉断D、无法确定哪条绳子先被拉断GOMNNGG1G2A例4.重15N的物体由OP、OM两条绳拉住，OP与竖直方向成θ角，若OP、OM能承受的最大拉力分别为10N和15N。问为了保持绳不被拉断，θ角的最大值等于多少？3POMGF1F2例5.如图所示，绳长AB=8m，轻杆BC=12m，墙上的两固定点AC=15m，所挂物体的重量G=60N。求绳受到的拉力与杆受到的压力。GFACAB1ABCGF1F2由力三角形BF1G和几何三角形ABC相似，则有：GFACBC2NNGACABF32601581NNGACBCF486015122例6.一只球重G=20N，静止于两个相交的光滑斜面之间，如图所示，当两斜面倾角分别为α=37°和β=53°时，求球对每一斜面的压力大小。βαGG1G2例7.在倾角α=30°的斜面上，有一块竖直放置的档板，在档板和斜面之间有一个重为G=20N的光滑圆球，如图所示，试求球对斜面的压力和对档板的压力。α例8.如图所示，一个半径为R，重为G的圆球，被用长度L的细绳挂在竖直光滑的墙上。若L增长，则绳对球的拉力F1和对竖直墙壁的压力F2的变化是（）A、F...