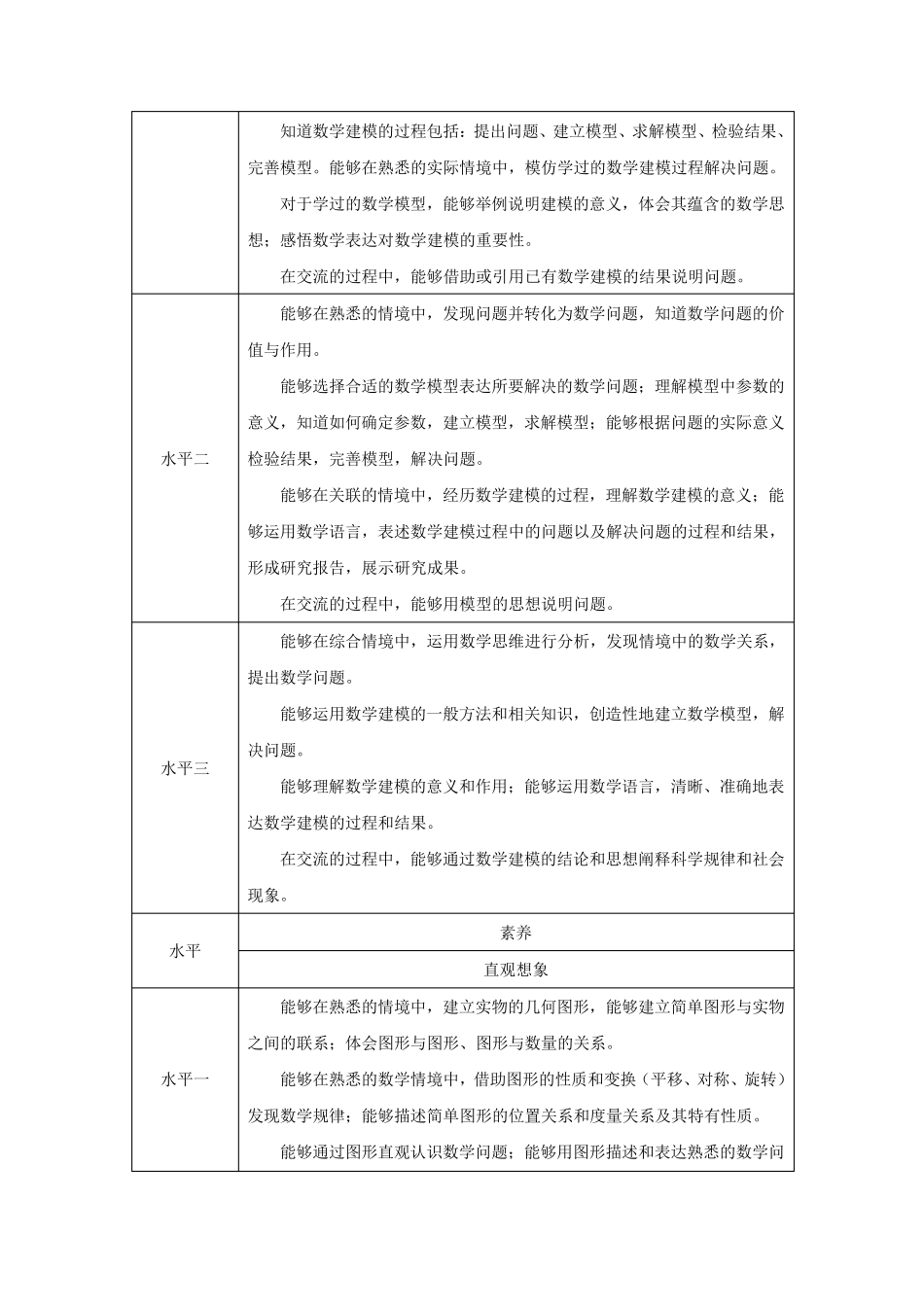
一、数学学科核心素养的水平划分 水平 素养 数学抽象 水平一 能够在熟悉的情境中直接抽象出数学概念和规则,能够在特例的基础上归纳并形成简单的数学命题,能够模仿学过的数学方法解决简单问题。 能够解释数学概念和规则的含义,了解数学命题的条件与结论,能够在熟悉的情境中抽象出数学问题。 能够了解用数学语言表达的推理和论证;能够在解决相似的问题中感悟数学的通性通法,体会其中的数学思想。 在交流的过程中,结合实际情境解释相关的抽象概念。 水平二 能够在关联的情境中抽象出一般的数学概念和规则,能够将已知数学命题推广到更一般的情形,能够在新的情境中选择和运用数学方法解决问题。 能够用恰当的例子解释抽象的数学概念和规则;理解数学命题的条件与结论;能够理解和构建相关数学知识之间的联系。 能够理解用数学语言表达的概念、规则、推理和论证;能够提炼出解决一类问题的数学方法,理解其中的数学思想。 在交流的过程中,能够用一般的概念解释具体现象。 水平三 能够在综合的情境中抽象出数学问题,并用恰当的数学语言予以表达;能够在得到的数学结论基础上形成新命题;能够针对具体问题运用或创造数学方法解决问题。 能够通过数学对象、运算或关系理解数学的抽象结构,能够理解数学结论的一般性,能够感悟高度概括、有序多级的数学知识体系。 在现实问题中,能够把握研究对象的数学特征,并用准确的数学语言予以表达;能够感悟通性通法的数学原理和其中蕴含的数学思想。 在交流的过程中,能够用数学原理解释自然现象和社会现象。 水平 素养 逻辑推理 水平一 能够在熟悉的情境中,用归纳或类比的方法,发现数量或图形的性质、数量关系或图形关系。 能够在熟悉的数学内容中,识别归纳推理、类比推理、演绎推理;知道通过归纳推理、类比推理得到的结论是或然成立的,通过演绎推理得到的结论是必然成立的。能够通过熟悉的例子理解归纳推理、类比推理和演绎推理的基本形式。了解熟悉的数学命题的条件与结论之间的逻辑关系;能够证明简单的数学命题并有条理地表述论证过程。 能够了解熟悉的概念、定理之间的逻辑关系。 能够在交流过程中,明确所讨论问题的内涵,有条理地表达观点。 水平二 能够在关联的情境中,发现并提出数学问题,用数学语言予以表达;能够理解归纳、类比是发现和提出数学命题的重要途径。 能够对与学过的知识有关联的数学命题,通过对条件与结果的分析,探索论证的思路,选择合适...