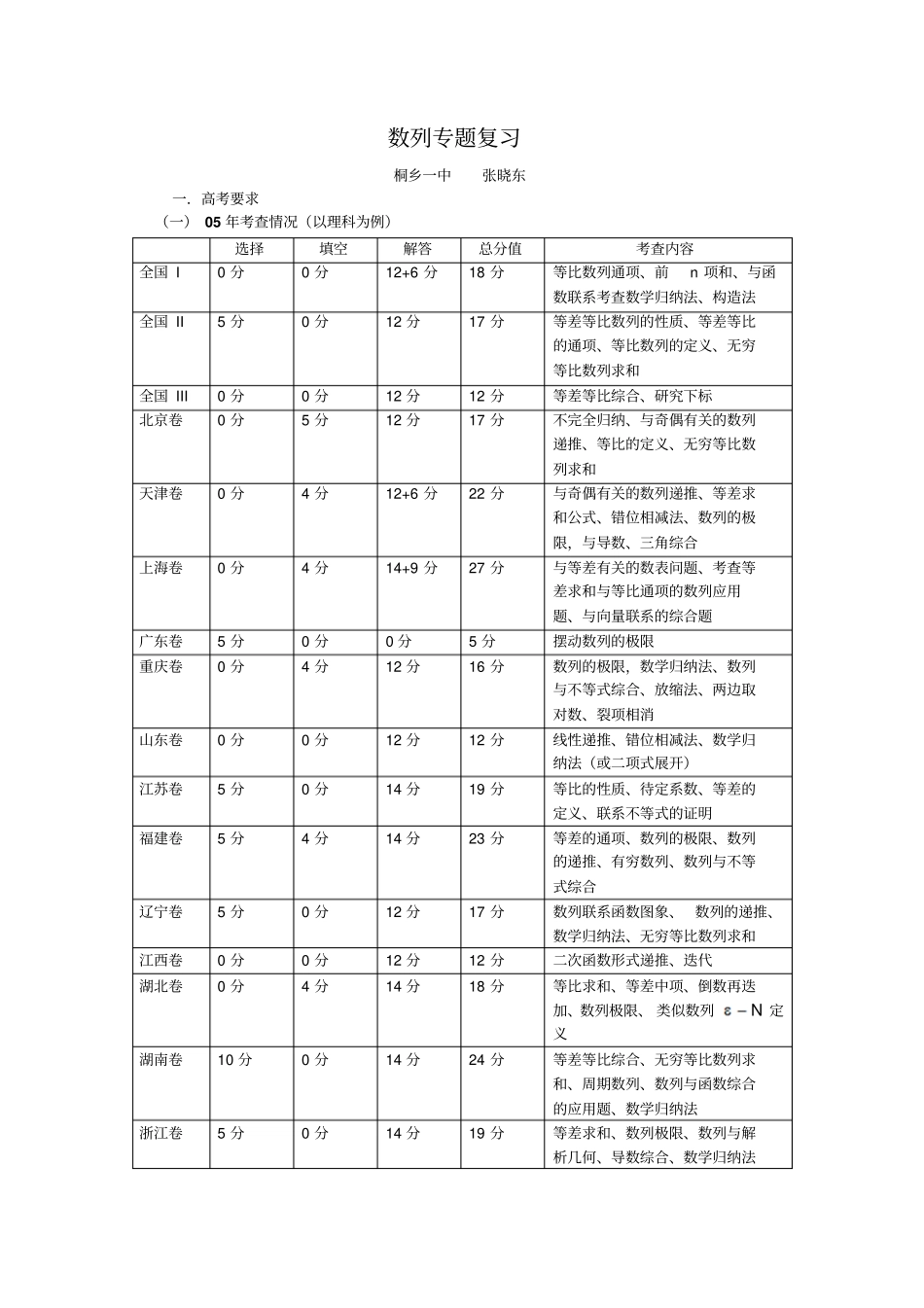
数列专题复习桐乡一中张晓东一.高考要求(一) 05 年考查情况(以理科为例)选择填空解答总分值考查内容全国 I 0 分0 分12+6 分18 分等比数列通项、前n 项和、与函数联系考查数学归纳法、构造法全国 II 5 分0 分12 分17 分等差等比数列的性质、等差等比的通项、等比数列的定义、无穷等比数列求和全国 III 0 分0 分12 分12 分等差等比综合、研究下标北京卷0 分5 分12 分17 分不完全归纳、与奇偶有关的数列递推、等比的定义、无穷等比数列求和天津卷0 分4 分12+6 分22 分与奇偶有关的数列递推、等差求和公式、错位相减法、数列的极限,与导数、三角综合上海卷0 分4 分14+9 分27 分与等差有关的数表问题、考查等差求和与等比通项的数列应用题、与向量联系的综合题广东卷5 分0 分0 分5 分摆动数列的极限重庆卷0 分4 分12 分16 分数列的极限,数学归纳法、数列与不等式综合、放缩法、两边取对数、裂项相消山东卷0 分0 分12 分12 分线性递推、错位相减法、数学归纳法(或二项式展开)江苏卷5 分0 分14 分19 分等比的性质、待定系数、等差的定义、联系不等式的证明福建卷5 分4 分14 分23 分等差的通项、数列的极限、数列的递推、有穷数列、数列与不等式综合辽宁卷5 分0 分12 分17 分数列联系函数图象、 数列的递推、数学归纳法、无穷等比数列求和江西卷0 分0 分12 分12 分二次函数形式递推、迭代湖北卷0 分4 分14 分18 分等比求和、等差中项、倒数再迭加、数列极限、 类似数列N 定义湖南卷10 分0 分14 分24 分等差等比综合、无穷等比数列求和、周期数列、数列与函数综合的应用题、数学归纳法浙江卷5 分0 分14 分19 分等差求和、数列极限、数列与解析几何、导数综合、数学归纳法(二)教学要求:1.等差数列与等比数列是两种最基本、最重要及应用最广泛的数列,其他数列问题的解决往往借助它们完成,或经过变形转化为等差或等比数列,或利用等差、 等比数列的研究方法。所以等差数列与等比数列的基础知识是数列中最基本、最重要也最易把握的知识。2.数列的通项是数列最重要、最常见的表达形式,它是数列的核心。应弄清通项公式的意义——项数n的函数;理解通项公式的作用——可以用通项公式求数列的任意一项的值及对数列进行一般性的研究。3.数列的递推式是数列的另一种表达形式,可以是一阶线性递推、二阶线性递推、二次函数形式递推、勾函数形式递推、与奇偶联系的递推...