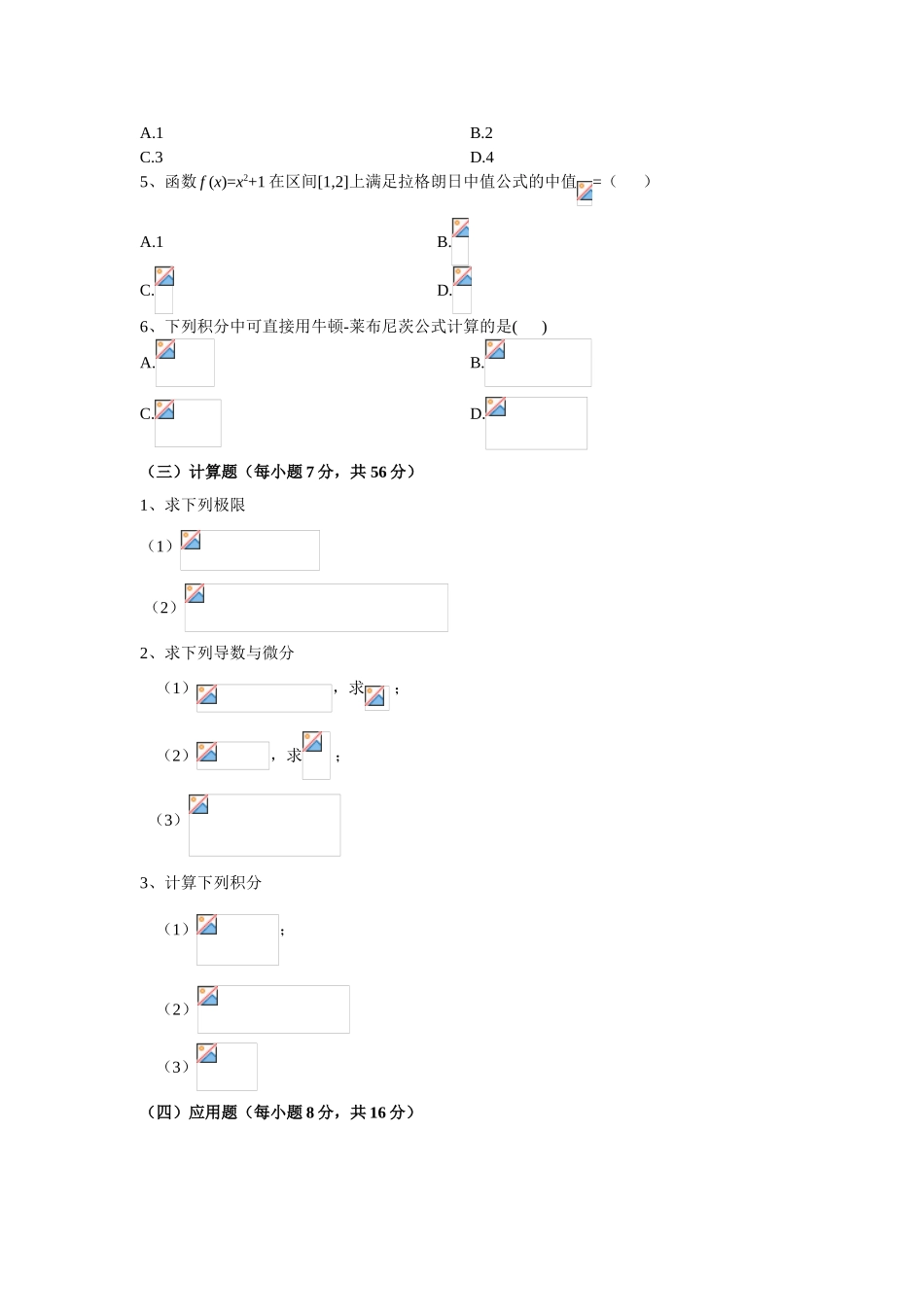
(一)填空题(每小题 2 分,共 16 分)1、函数的反函数为 .2、3、已知 ,那么 .4、函数 ,在内持续,则 .5、曲线在处的切线方程为 .6、 .7、 .8、 .(二)单选(每小题 2 分,共 12 分。在每小题给出的选项中,选出对的答案)1、函数 y=f(x)的图形如图所示,则它的值域为( )A.[1,4)B.[1,4]C.[1,5)D.[1,5]2、当时,下列变量为无穷小量的是( )A.B.ln xC.x sinD.3、设函数 f(x)可导,且,则曲线 y=f(x)在点(1,f(1))处的切线斜率为( )A.1B.0C.-1D.-24、曲线的渐近线的条数为 ( )A.1B.2C.3D.45、函数 f (x)=x2+1 在区间[1,2]上满足拉格朗日中值公式的中值=( )A.1B.C.D.6、下列积分中可直接用牛顿-莱布尼茨公式计算的是( )A.B.C.D.(三)计算题(每小题 7 分,共 56 分)1、求下列极限(1) (2)2、求下列导数与微分(1),求 ; (2),求 ; (3)3、计算下列积分(1); (2) (3)(四)应用题(每小题 8 分,共 16 分)1、求极限参考答案一、填空题(每空 2 分,共 16 分)1、2、03、14、2 5、 6、 7、 8、二、单选题(每小题 2 分,共 12 分。在每小题给出的选项中,只有一项是符合题目规定的。多选不给分)1.(A) 2.(C) 3.(C) 4.(B)5.(D)6.(D)三、计算题(每小题 7 分,共 56 分)1、(1) 0(2) 2、(1)(2) (3)3、(1) (2) (3) 四、应用题(每小题 8 分,共 16 分)1、-1/122、略