线性代数习题册参考解答VIP免费

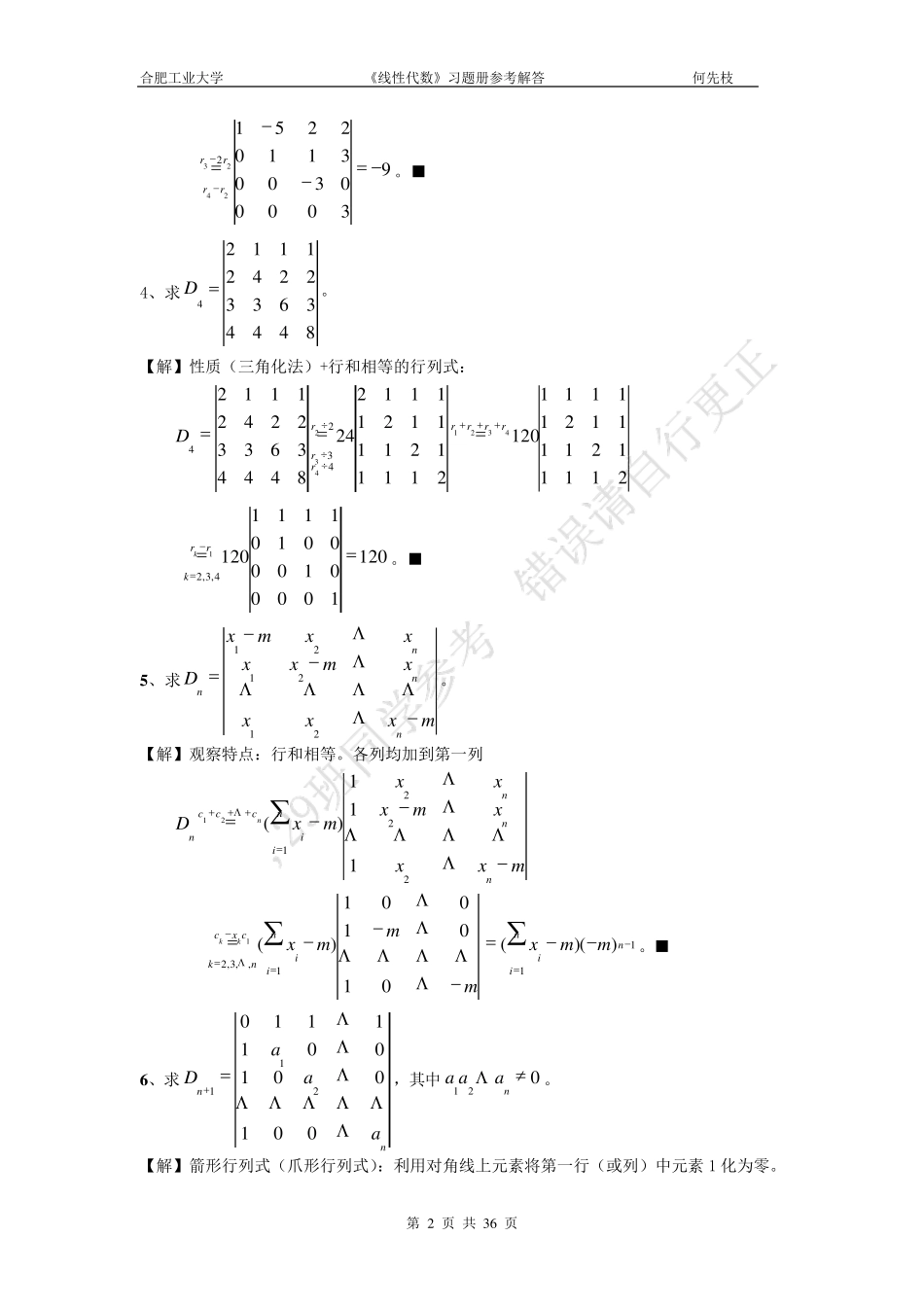
合肥工业大学 《线性代数》习题册参考解答 何先枝 第 1 页 共 36 页 第一章 行列式 1 、求下列排列的逆序数，并确定它们的奇偶性。 （1 ）1 3 4 7 2 6 5 ；（2 ）321)1(nn。 【解】（1）62130000)1347265(，偶排列； （2）2)1()1(210]321)1([nnnnn。 当14,4kkn时，)14(2),14(22)1(kkkknn为偶数，即为偶排列； 当34,24kkn时，)34)(12(),14)(12(2)1(kkkknn为奇数，即为奇排列。■ 2 、用行列式定义计算 xxxxxxf111123111212)( 中4x 和3x 的系数，并说明理由。 【解】由行列式定义可知： 含4x 有的项只能是主对角线元素乘积，故4x 的系数为2 ； 含有3x 的项只能是（1 ，2 ），（2 ，1 ），（3 ，3 ），（4 ，4 ）的元素乘积项，而 10010)2134(， 故3x 的系数为1 .■ 3、求21647295417321524D。 【解】三角化法： 611061203110225161103110612022516011301160212152323112241324rrccrrrrrrD 合肥工业大学 《线性代数》习题册参考解答 何先枝 第 2 页 共 3 6 页 9300003003110225123242rrrr。■ 4、求84443633224211124 D。 【解】性质（三角化法）+行和相等的行列式： 21111211112111111 2 021111211112111122 4844436332242111243212432434rrrrrrrD 1 2 010000100001011111 2 014,3,2rrkk。■ 5 、求mxxxxmxxxxmxDnnnn212121。 【解】观察特点：行和相等。各列均加到第一列 mxxxmxxxmxDnnnniicccnn2221111)(21 mmmxniicxcnkkk0101001)(1,,3,2111))(( nniimmx。■ 6 、求nnaaaD0010010011110211 ，其中021naaa。 【解】箭形行列式（爪形行列式）：利用对角线上元素将第一行（或列）中元素 1 化为零。 合肥工业大学 《线性代数》习题册参考解答 何先枝 第 3 页 共 3 6 页 为此，第一列减去第k 列的ka1（nk,,3,2）可得： nniinniinaaaaaaaaD2112111)1(0000000001111。■ 7 、求7111141111311112D。 【解】降阶法。 713143115713114311151000171111411113100217111141...