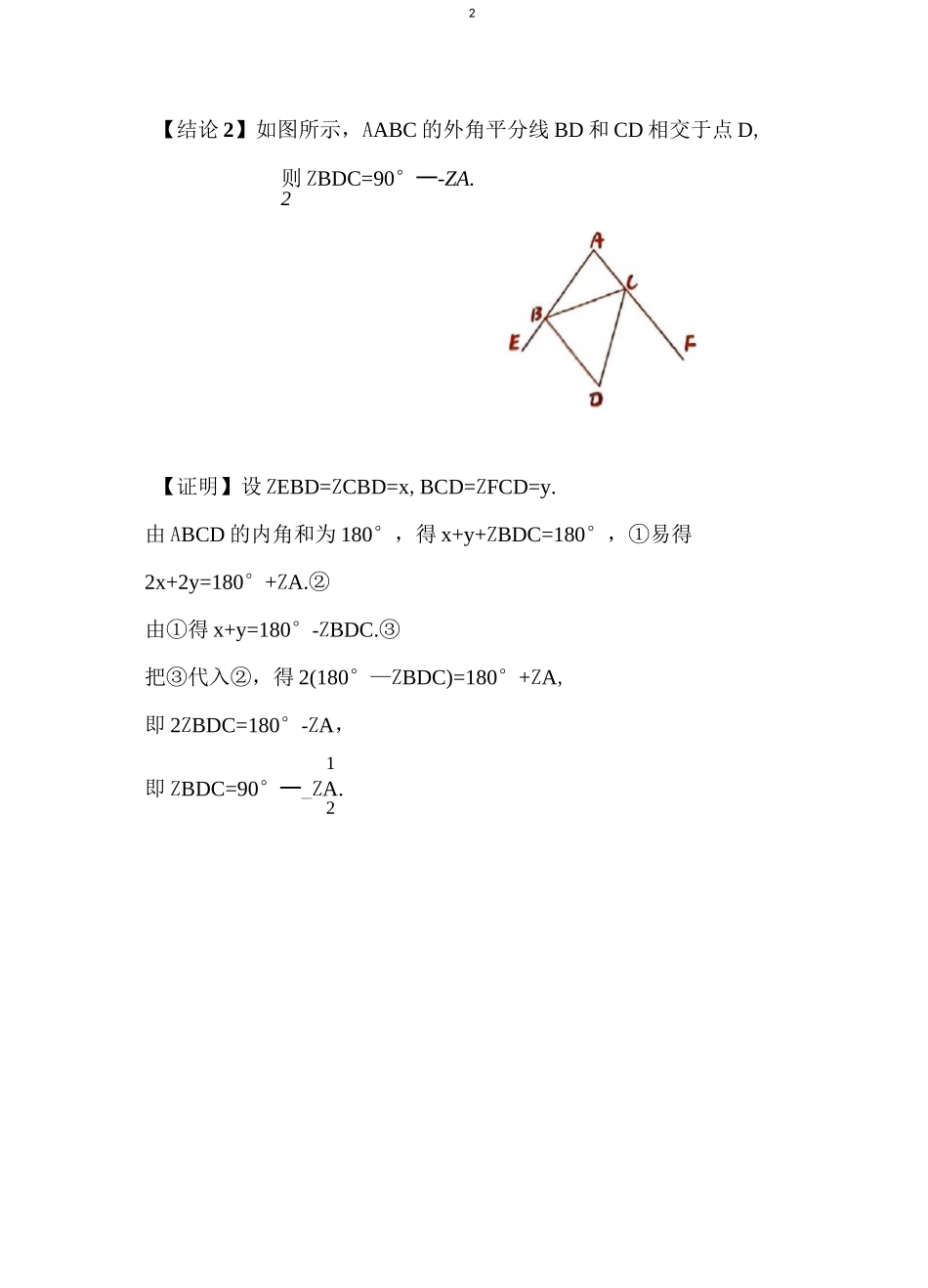
1双角平分线模型模型讲解【结论 1】如图所示,在厶 ABC 中,BD,CD 分别是 ZABC 和 ZACB1的平分线,则 ZBDC=90°+-ZA.2【证明】设 ZABD=ZDBC=x,ZACD=ZBCD=y.由厶 ABC 的内角和为180。,得 ZA+2x+2y=180°.① 由厶 BDC 的内角和为 180°,得ZBDC+x+y=180°.② 由②得 x+y=180°-ZBDC.③把③代入①,得 ZA+2(180°-ZBDC)=180°,即 2ZBDC=180°+ZA,1即 ZBDC=90°+-ZA.2【结论 2】如图所示,AABC 的外角平分线 BD 和 CD 相交于点 D,则 ZBDC=90°一-ZA.2【证明】设 ZEBD=ZCBD=x,BCD=ZFCD=y.由 ABCD 的内角和为 180°,得 x+y+ZBDC=180°,①易得2x+2y=180°+ZA.②由①得 x+y=180°-ZBDC.③把③代入②,得 2(180°—ZBDC)=180°+ZA,即 2ZBDC=180°-ZA,1即 ZBDC=90°一_ZA.23【结论 3】如图所示,AABC 的内角平分线 BD 和外角平分线 CD 相1交于点 D,贝 UZD=2ZA.【证明】设 ZABD=ZDBC=x,ZACD=ZECD=y.由外角定理得 2y=ZA+2x,①y=ZD+x.②把②代入①,得 2(ZD+x)=ZA+2x,1即 ZD=-ZA.A.130B.120°C.100°D.904典型例题典例 1 如图,在△ABC 中,ZABC 和 ZACB 的平分线相交于点 O,若ZBAC=80°,则 ZBOC 的度数是().典例 2如图,BA1和 CA],分别是△ABC 的内角平分线和外角平分线,BA2是 ZA1BD 的平分线,CA2是 ZA1CD 的平分线,BA3是 ZA2BD 的平分线,CA3是 ZA2CD 的平分线,……以此类推,若 ZA=a,则 A2020典例 3【问题】如图 1,在厶 ABC 中,BE 平分 ZABC,CE 平分 ZACB.5若 ZA=80°,则 ZBEC=;若 ZA=n。,则 ZBEC=.【探究】(1) 如图 2,在厶 ABC 中,BD,BE 三等分 ZABC,CD,CE 三等分ZACB,若 ZA=n°,贝 ljZBEC=;(2) 如图 3,0 是 ZABC 的平分线 BO 与 ZACD 的平分线 CO 的交点,试分析 ZBOC 和 ZA 有怎样的关系,并说明理由;(3) 如图 4,O 是三角形 ABC 的外角 ZDBC 与 ZBCE 的平分线 BO 和CO 的交点,则 ZBOC 与 ZA 有怎样的关系?(只写结论,不需要证明)A.121°B.120C.119°D.1186初露锋芒1.如图所示,在厶 ABC 中,ZABC,ZACB 的平分线 BE,CD 相交于点F,若 ZA=60°,则 ZBFC 等于().2.如图,五边形 ABCDE 在 ZBCD,ZEDC 处的外角分别是 ZFCD,ZGDC,CP,DP 分别平分 ZFCD 和 ZGDC 且相交于点 P.若 ZA=160°,ZB=80°,ZE=90°,则 ZCPD=.A.15°B.30°C.45°D.607感受中考1.(2019 黑龙江大庆中考真题)如图...