线面垂直的性质VIP免费

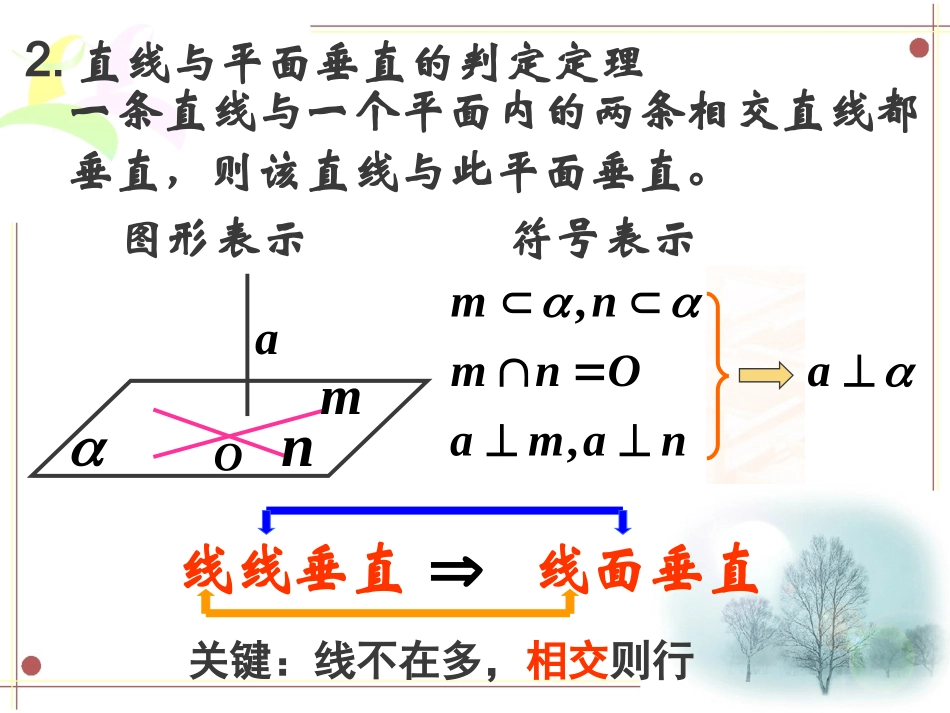
1.直线和平面垂直的定义？如果直线和这个平面内的任意一条直线都垂直,则称这条直线和这个平面垂直.,.lblb若则注:αlAb一、知识回顾2.直线与平面垂直的判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。,,mnmnOaaman线线垂直线面垂直图形表示符号表示amnO关键：线不在多，相交则行如图，长方体ABCD—A1B1C1D1中，棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何？它们彼此之间具有什么位置关系？AA1BCDB1C1D1二、新知探究3线面垂直的性质定理：符号语言：图形语言：垂直于同一平面的两直线互相平行.//abab，abα记直线b和α的交点为o,则可过o作b’∥a.垂直于同一个平面的两条直线平行αabo证明：假设a与b不平行.∴b’⊥α.∴过点o的两条直线b和b’都垂直平面α,这不可能!b’已知:a⊥α,b⊥α,求证:a//b a⊥α,∴a∥b.反证法否定结论正确推理肯定结论导出矛盾记直线b和α的交点为o,则可过o作b’∥a.线面垂直的性质定理：垂直于同一个平面的两条直线平行αabo证明：假设a与b不平行.∴b’⊥α.∴过点o的两条直线b和b’都垂直平面α,这不可能!b’已知:a⊥α,b⊥α,求证:a//b a⊥α,∴a∥b.反证法否定结论正确推理肯定结论导出矛盾推论推论11：直线与平面垂直的性质：直线与平面垂直的性质如果一条直线垂直于一个平面，那么这条直线垂直于面上任意直线．（定义）简述为：线面垂直线线垂直符号语言：abab图形语言：αba推论2：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面．符号语言：//abab图形语言：abO直线与平面垂直的性质：直线与平面垂直的性质：2、如果一条直线垂直于一个平面，那么这条直线垂直于面上任意直线．（定义）3、如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面．1、垂直于同一个平面的两条直线平行随堂测试1.判断下列命题是否正确：①平行于同一条直线的两条直线互相平行;②垂直于同一条直线的两条直线互相平行;③平行于同一个平面的两条直线互相平行；④垂直于同一个平面的两条直线互相平行.正确的是：①④2.若a,b表示直线,表示平面，下列命题正确的是。//b,,)1(则baa(3)//,b,baa则(4),,baba则b,,//)2(则baa(3)(4)3、判断下列命题是否正确；（1）垂直于同一条直线的两个平面互相平行；（）（2）垂直于同一个平面的两条直线互相平行；（）（3）一条直线在平面内，另一条直线与这个平面垂直，则这两条直线互相垂直。（）4、已知直线a、b和平面α，且ab⊥，aα⊥，则b与α的位置关系________________________√√√bb或//例1:如图，已知于点A，于点B，求证：.,lCACB,,aaAB//alABαβCla三、理论迁移例2如图，已知矩形ABCD所在平面，M、N分别是AB、PC的中点。求证：（1）PA;MNCD（2）若，求证：MN面PCD45PDAPABCDMNEABCDA1B1C1D1MNO1、如图所示，在正方体ABCD-中，M是AB上一点，N是C的中点，MN⊥平面DC求证：(1)MNA∥(2)M是AB的中点.1111DCBA1A1A1D2.数学思想转化空间问题平面问题1.知识方法小结①线面垂直的性质定理及其应用③类比探究，逆向探究垂直关系平行关系线面关系线线关系1.类比探究：①交换“平行”与“垂直”a⊥α,b⊥αa∥b性质定理：变式探究a⊥α,b⊥αa∥b1.类比探究：①交换“平行”与“垂直”a⊥α,b⊥αa∥ba⊥α,b⊥αa∥b性质定理：变式探究a⊥α,b⊥αa∥b?1.类比探究：①交换“平行”与“垂直”a⊥α,b∥αa⊥ba⊥α,b⊥αa∥b性质定理：a⊥α,b⊥αa∥babαl变式探究②交换“直线”与“平面”1.类比探究：①交换“平行”与“垂直”a⊥α,b∥αa⊥b②交换“直线”与“平面”a⊥α,b⊥αa∥b性质定理：a⊥α,b∥αa⊥b变式探究a⊥α,1.类比探究：①交换“平行”与“垂直”bb∥αa⊥a⊥α,b∥αa⊥b②交换“直线”与“平面”a⊥α,b⊥αa∥b性质定理：a⊥α,b∥αa⊥bββ变式探究a⊥α,1.类比探究：①交换“平行”与“垂直”∥αa⊥a⊥α,b∥αa⊥b②交换“直线”与“平面”a⊥α,b⊥αa∥...