递推最小二乘法VIP免费

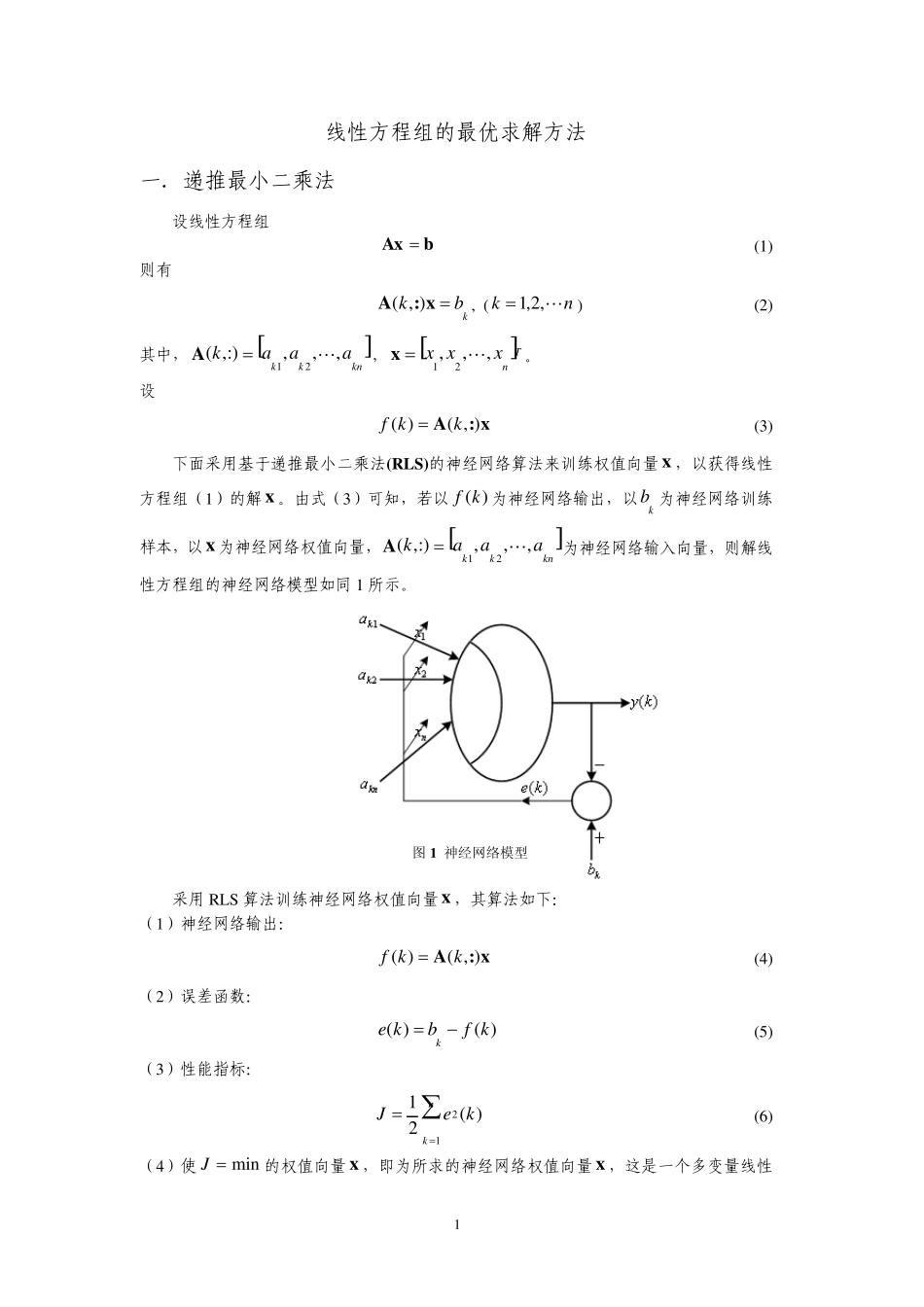
1 线性方程组的最优求解方法 一．递推最小二乘法 设线性方程组 bAx  (1) 则有 kbkx:A),(, (nk,2,1) (2) 其中， knkkaaak,,,:),(21A，Tnxxx,,,21x。 设 x:A),()(kkf (3) 下面采用基于递推最小二乘法(RLS)的神经网络算法来训练权值向量 x，以获得线性方程组（1）的解x。由式（3）可知，若以)(kf为神经网络输出，以kb 为神经网络训练样本，以x为神经网络权值向量， knkkaaak,,,:),(21A为神经网络输入向量，则解线性方程组的神经网络模型如同 1 所示。 图 1 神经网络模型 采用 RLS 算法训练神经网络权值向量x，其算法如下： （1）神经网络输出： x:A),()(kkf (4) （2）误差函数： )()(kfbkek  (5) （3）性能指标： nkkeJ12)(21 (6) （4）使minJ的权值向量 x，即为所求的神经网络权值向量 x，这是一个多变量线性 2 优化问题，为此，由 0xJ 可得最小二乘递推法（RLS）： ]),([1kkkkkkbx:AQxx (7) ),(),(1),(:AP:A:APQkkkTkTkk (8) kkkkP:AQIP)],([1 (9) nk,,2,1 随机产生初始权值向量)1,(0nrandx，设nnRIP0（ 是足够大的正数（一般取10610~10）， nn RI是单位矩阵），通过对样本数据训练，即可获得神经网络权值向量x，此即为线性方程组（1）的解。 二．具有遗忘因子的递推最小二乘估计公式为： ]),([1kkkkkkbx:AQxx (10) ),(),(),(:AP:A:APQkkkTkTkk  (11) kkkkP:AQIP)],([11 (12) 式中，1:)],(:),([)(kAkAkTWP，W 为加权对角阵： 10021nnW （nnRIP0，10610~10）。 几点说明： (1) 当1时，该估计公式组为基本递推最小二乘算法； (2)  的选择范围一般在：99.095.0 。当参数变化快时， 取小点；变化慢时，取大点； 3 三．共轭梯度法及其应用 设线性方程组bAx ，则有 给定初始近似0x ，取000Axbrp 对,2,1,0k计算： kTkkTkkApppr kkkkpxx1 kkkkkAprbAxr11，且bAxrkk kTkkTkkAppApr1 kkkkprp11。 几点说明： 1. 应用共轭梯度法求解实对称正定线性方程组，不必事先估计方程组的系数矩阵A 的特征值的上、下界，不需要选取任何迭代参数，使用方便。而且，它的收敛速度较快，对于非坏...