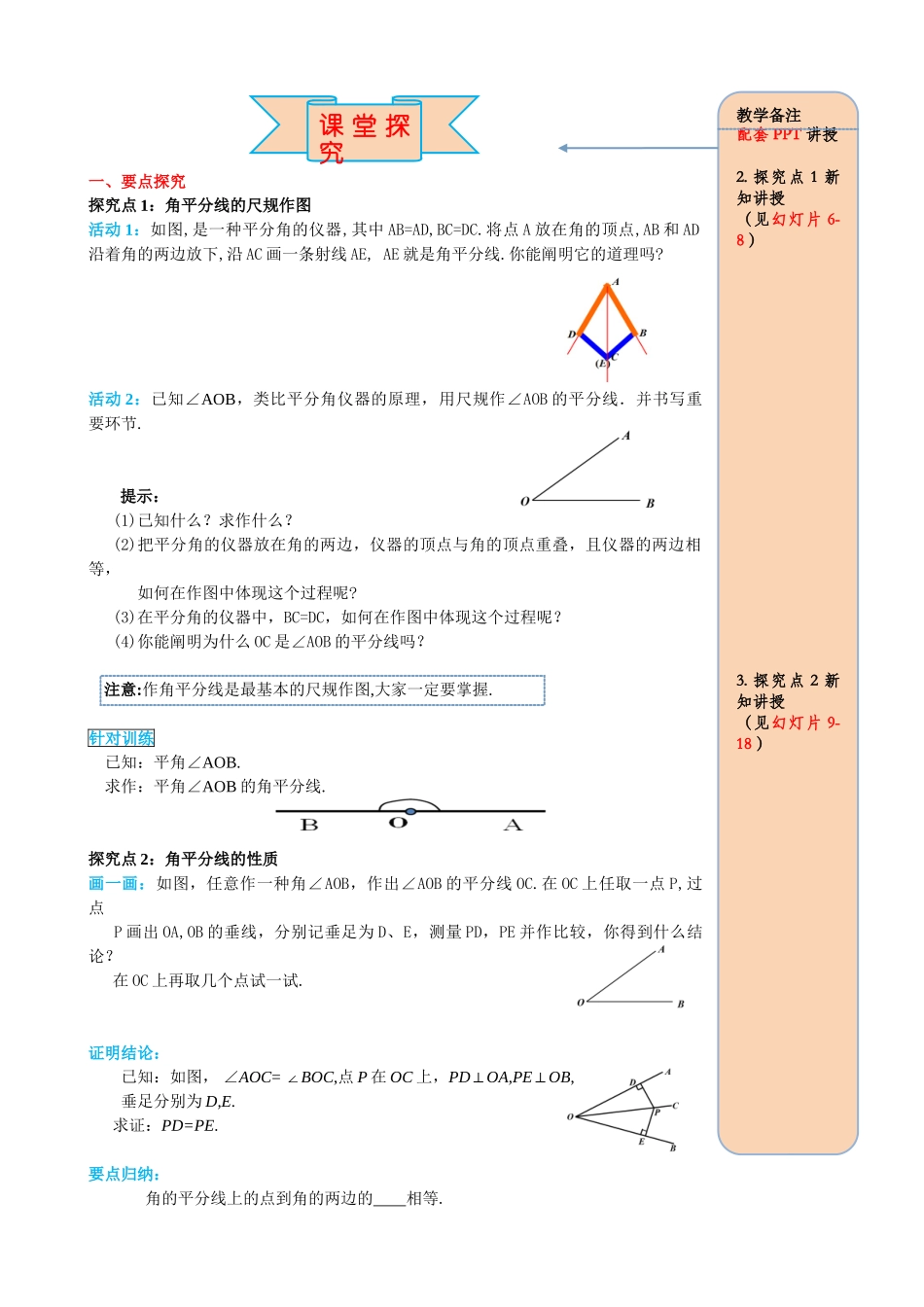
第十二章 全等三角形 12.3 角平分线的性质 第 1 学时 角平分线的性质学习目的:1.通过操作、验证等方式,探究并掌握角平分线的性质定理. 2.能运用角的平分线性质解决简朴的几何问题. 重点:掌握角的平分线的性质定理,用直尺和圆规作角的平分线.难点:角平分线定理的应用.一、知识链接1.鉴定两个三角形全等的办法有哪几个?2.如图,在△ABC 中,BD 平分∠ABC,则∠ =∠ . 过点 D 作 DE⊥BC,垂足为 E,则图中线段 的长度表达点 D 到 BC 的距离.二、新知预习1.OC 是∠AOB 的平分线,点 P 是射线 OC 上的任意一点,操作测量:取点 P 的三个不同的位置,分别过点 P 作 PD⊥OA,PE ⊥OB,点 D、E 为垂足,测量 PD、PE 的长.将三次数据填入下表:观察测量成果,猜想线段 PD 与 PE 的大小关系,写出结论 PD[来源:学科网]PE第一次第二次 第三次[来源:学,科,网 Z,X,X,K]2.下面四个图中,点 P 都在∠AOB 的平分线上,则 PD=PE 的是 ( ) A B C D3.猜想: 角平分线的性质:角平分线上任意一点到两边的 相等.三、我的疑惑______________________________________________________________________________________________________________________________________________________自 主 学习教学备注学 生 在 课 前完 毕 自 主 学习部分1. 复习引入( 见 幻 灯 片3-5 )一、要点探究探究点 1:角平分线的尺规作图活动 1:如图,是一种平分角的仪器,其中 AB=AD,BC=DC.将点 A 放在角的顶点,AB 和 AD沿着角的两边放下,沿 AC 画一条射线 AE, AE 就是角平分线.你能阐明它的道理吗? 活动 2:已知∠AOB,类比平分角仪器的原理,用尺规作∠AOB 的平分线.并书写重要环节.提示:(1)已知什么?求作什么?(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重叠,且仪器的两边相等, 如何在作图中体现这个过程呢?(3)在平分角的仪器中,BC=DC,如何在作图中体现这个过程呢?(4)你能阐明为什么 OC 是∠AOB 的平分线吗? 注意:作角平分线是最基本的尺规作图,大家一定要掌握.针对训练已知:平角∠AOB. 求作:平角∠AOB 的角平分线.探究点 2:角平分线的性质画一画:如图,任意作一种角∠AOB,作出∠AOB 的平分线 OC.在 OC 上任取一点 P,过点 P 画出 OA,OB 的垂线,分别记垂足为 D、E,测量 PD,PE 并作比较,你得到什么结论?在 OC 上再取几个点试一试....