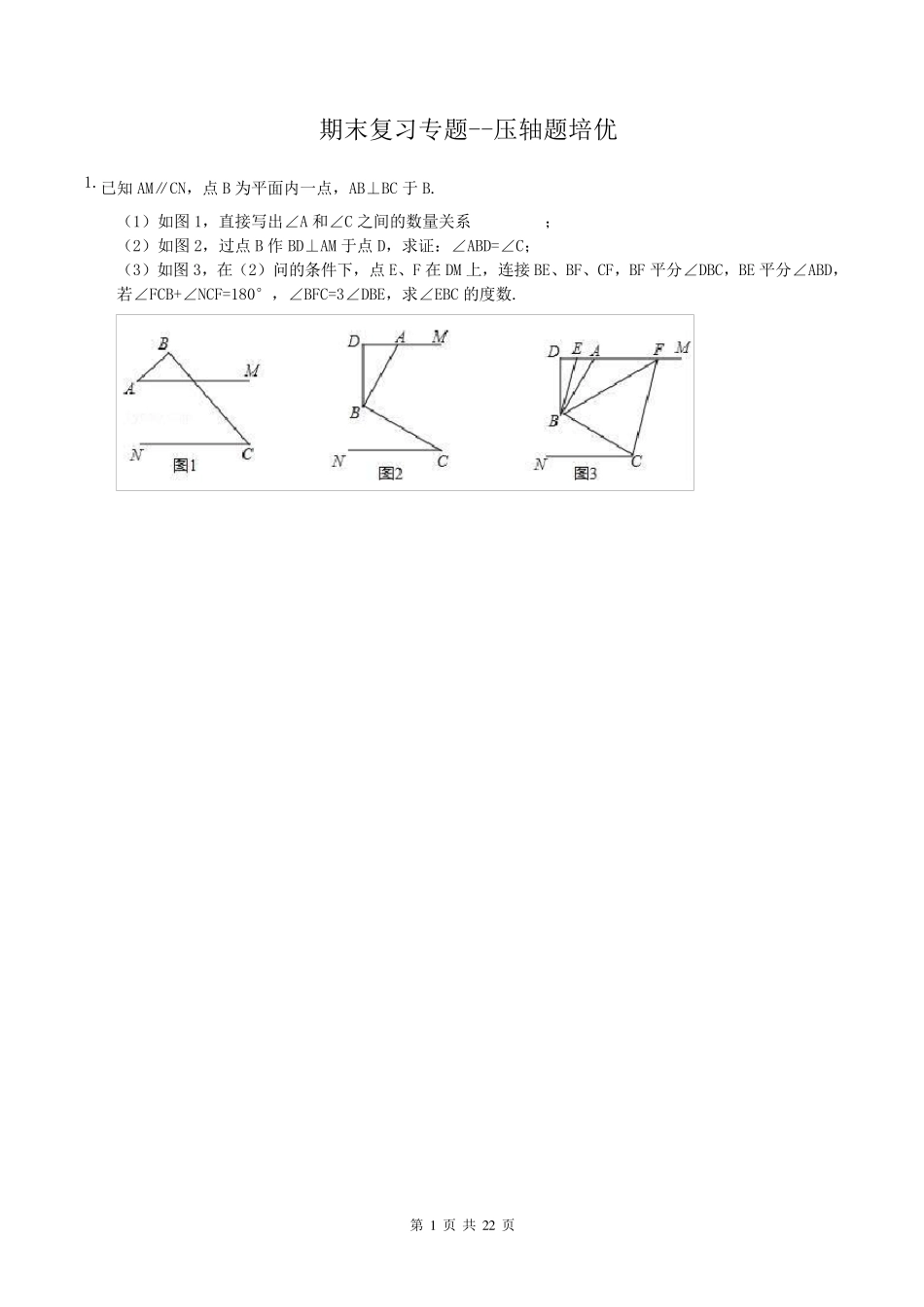
第 1 页 共 2 2 页 期末复习专题--压轴题培优 1.已知AM∥CN,点B 为平面内一点,AB⊥BC 于B. (1)如图1,直接写出∠A 和∠C 之间的数量关系 ; (2)如图2,过点B 作BD⊥AM 于点D,求证:∠ABD=∠C; (3)如图3,在(2)问的条件下,点E、F 在DM 上,连接BE、BF、CF,BF 平分∠DBC,BE 平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC 的度数. 第 2 页 共 2 2 页 2.如图,已知两条射线OM∥CN,动线段AB 的两个端点A.B 分别在射线OM、CN 上,且∠C=∠OAB=108°,F在线段CB 上,OB 平分∠AOF,OE 平分∠COF. (1)请在图中找出与∠AOC 相等的角,并说明理由; (2)若平行移动AB,那么∠OBC 与∠OFC 的度数比是否随着 AB 位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值; (3)在平行移动AB 的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA 度数;若不存在,说明理由. 第 3 页 共 2 2 页 3.已知AB∥CD,线段EF分别与AB、CD相交于点E、F. (1)如图①,当∠A=25°,∠APC=70°时,求∠C的度数; (2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A.∠APC与∠C之间有什么确定的相等关系?试证明你的结论. (3)如图③,当点P在线段FE的延长线上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立,试探究它们之间新的相等关系并证明. 第 4 页 共 2 2 页 4.如图1,在平面直角坐标系中,A(a,0)是x 轴正半轴上一点,C 是第四象限一点,CB⊥y 轴,交y 轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16. (1)求C 点坐标; (2)如图2,设D 为线段OB 上一动点,当AD⊥AC 时,∠ODA 的角平分线与∠CAE 的角平分线的反向延长线交于点P,求∠APD 的度数. (3)如图3,当D 点在线段OB 上运动时,作 DM⊥AD 交BC 于M 点,∠BMD、∠DAO 的平分线交于N 点,则 D 点在运动过程中,∠N 的大小是否变化?若不变,求出其值,若变化,说明理由. 第 5 页 共 2 2 页 5.已知BC∥OA,∠B=∠A=100°.试回答下列问题: (1)如图 1 所示,求证:OB∥AC; (2)如图 2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数; (3)在(2)的条件下,若平行移动AC,如图 3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值。 第 6 页 共 2 2 ...