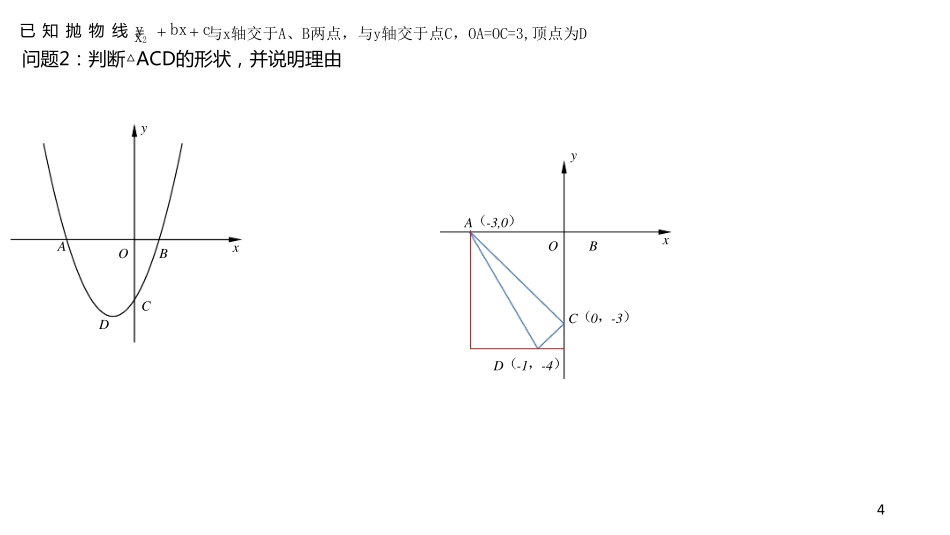
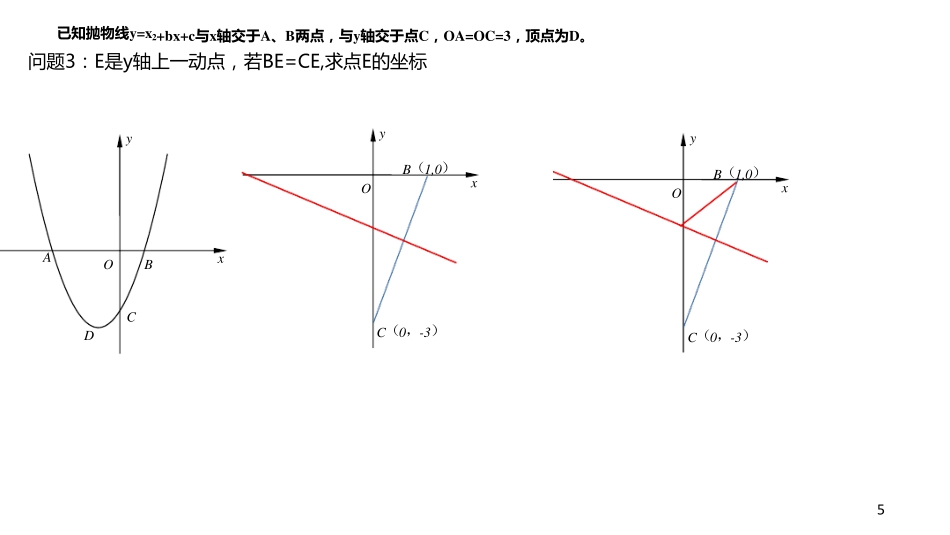
已 知 抛 物 线 y=x2+bx+c与 x轴 交 于 A、B两点,与 y轴 交 于 点C,OA=OC=3,顶点为D。 y A O B x C D 十字相乘 y ax2 bx c 2 1 y a(x x )(x x ) 问 题 1: 求 抛 物 线 解 析 式 和 顶 点 D坐 标 函数 点 形 配方法(★) y x2 2x 3 y (x 3)(x 1) y (x 1)2 4 y a(x h)2 k 原始三角形: 重视四点围成的三角形(边、角关系) x轴交点(x,0)、(x,0) 1 2 y轴交点(0,c) 顶点(h,k) 已 知 抛 物 线 y bx c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D x2 4 问 题 2: 判断 △ACD的 形 状 , 并 说 明 理 由 y y A O B x C D A(-3,0) O B x C(0,-3) D(-1,-4) 5 已 知 抛 物 线 y=x2+bx+c与 x轴 交 于 A、B两点,与 y轴 交 于 点C,OA=OC=3,顶点为D。 y B(1,0) O x C(0,-3) y B(1,0) O x C(0,-3) 问 题 3: E是 y轴 上 一动点,若BE=CE,求点E的坐标 y A O B x C D 6 已 知 抛 物 线 y=x2+bx+c与 x轴 交 于 A、B两点,与 y轴 交 于 点C,OA=OC=3,顶点为D。 问 题 4: 抛 物 线 上 有 一 动 点 P, 过 点 P作 PM⊥x轴于点 M,交直线 AC与点 N, 在线 段PM、MN中, 若其中一 条线 段是另一 条线 段的2倍, 求点 P的坐标。 y A O B x C D 7 已 知 抛 物 线 y=x2+bx+c与 x轴 交 于 A、B两点,与 y轴 交 于 点C,OA=OC=3,顶点为D。 y E A F O B x H P C D y E A F O B x H P C D 问 题 5: 直 线 AC下 方 的 抛 物 线 上 有 一 动 点 P, 过 点 P作 PH⊥AC于H, 求线 段PH的最大值及此时点 P的 坐标 y A O B x H P C D 8 已 知 抛 物 线 y=x2+bx+c与 x轴 交 于 A、B两点,与 y轴 交 于 点C,OA=OC=3,顶点为D。 y A G O B x E H P C D 问 题 6: 直 线 AC下 方 的 抛 物 线 上 有 一 动 点 P, 过 点 P作 PH⊥AC于 H, PG∥y轴 交 AC 于 G, PH为 邻 边 作 矩 形 PEGH, 求 矩 形 PEGH周 长 的 最 大 值 。 y A O B x C D 9 已 知 抛 物 线 y=x2+bx+c与...