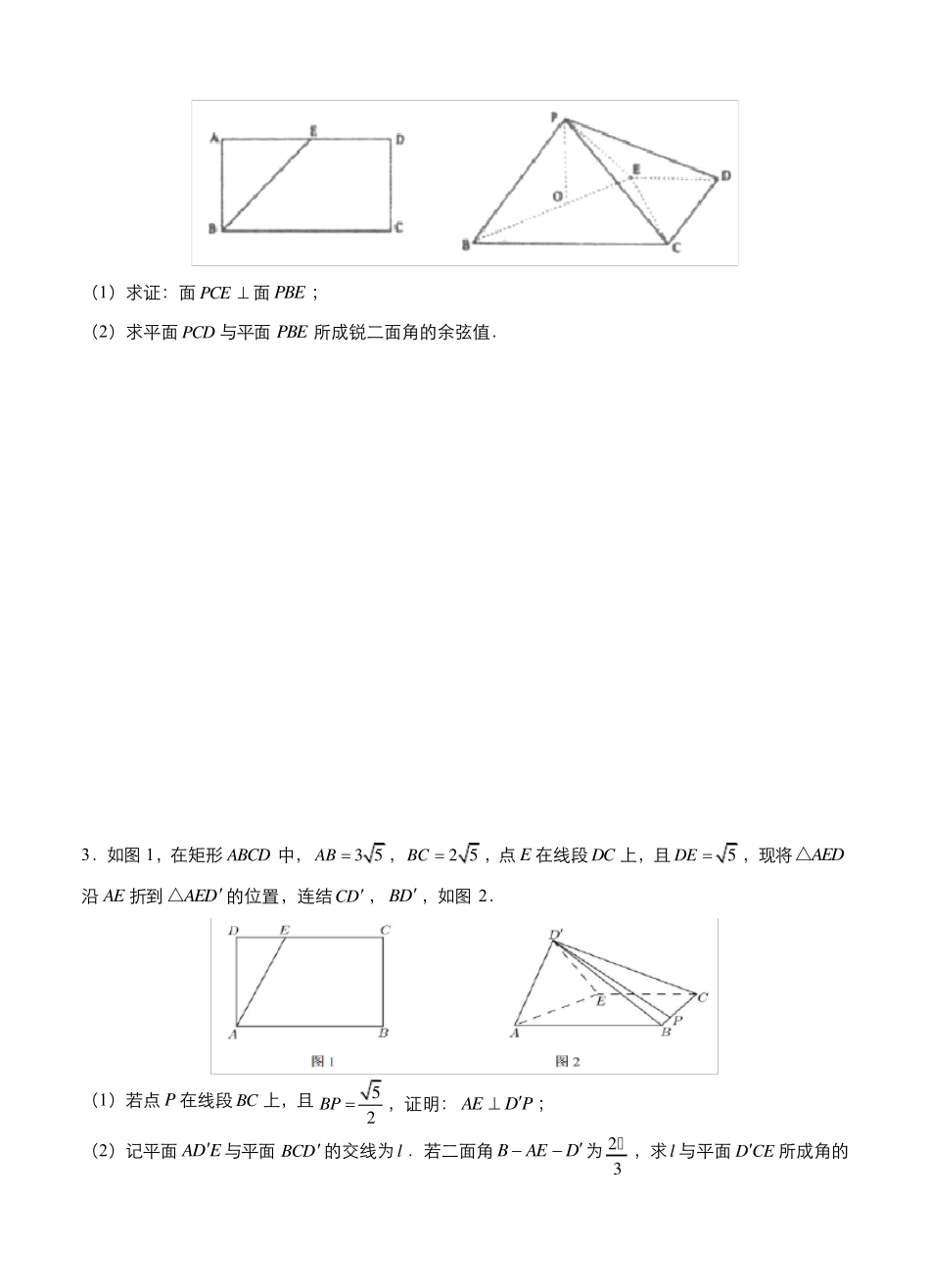
2020 年高考数学立体几何建系困难问大题精做 1.已知三棱锥 PABC(如图一)的平面展开图(如图二)中,四边形 ABCD 为边长等于2 的正方形,ABE△和BCF△均为正三角形,在三棱锥 PABC中: (1)证明:平面 PAC 平面 ABC ; (2)若点 M 在棱 PA 上运动,当直线 BM 与平面 PAC 所成的角最大时,求二面角 PBCM的余弦值. 图一 图二 2.矩形 ABCD 中,1AB ,2AD ,点 E 为 AD 中点,沿 BE 将ABE△折起至PBE△,如图所示,点 P在面 BCDE 的射影O 落在 BE 上. (1)求证:面 PCE 面 PBE ; (2)求平面 PCD 与平面 PBE 所成锐二面角的余弦值. 3.如图 1,在矩形 ABCD 中,35AB ,25BC ,点 E 在线段 DC 上,且5DE ,现将AED△沿 AE 折到AED△的位置,连结CD , BD ,如图 2. (1)若点 P 在线段 BC 上,且52BP ,证明: AED P ; (2)记平面 AD E 与平面 BCD 的交线为l.若二面角 BAED为 2 π3,求l与平面 D CE所成角的 正弦值. 4.如图,在四棱锥 PABCD中,已知底面 ABCD 是边长为 1 的正方形,侧面 PAD 平面 ABCD ,PAPD, PA 与平面 PBC 所成角的正弦值为2 17. (1)求侧棱 PA 的长; (2)设 E为 AB 中点,若 PAAB,求二面角 BPCE的余弦值. 1 .【答案】(1)见解析;(2) 5 3333. 【解析】(1)设 AC 的中点为O ,连接 BO , PO . 由题意,得2PAPBPC,1PO , 1AOBOCO . 在PAC△中, PAPC,O 为 AC 的中点,∴POAC, 在POB△中,1PO ,1OB ,2PB ,222POOBPB,∴POOB. ACOBO, AC , OB 平面,∴PO 平面 ABC , PO 平面 PAC ,∴平面 PAC 平面 ABC . (2)由(1)知, BOPO, BOAC, BO 平面 PAC , ∴BMO是直线 BM 与平面 PAC 所成的角,且1tanBOBMOOMOM, ∴当OM 最短时,即 M 是 PA 的中点时,BMO最大. 由 PO 平面 ABC ,OBAC,∴POOB, POOC, 于是以 OC ,OB ,OD 所在直线分别为 x 轴, y 轴, z 轴建立如图示空间直角坐标系, 则 0,0,0O, 1,0,0C, 0,1,0B, 1,0,0A , 0,0,1P,11,0,22M , 1, 1,0BC ...