2021.03.19八仙过海初中数学8大类几何模型附例题精编VIP免费

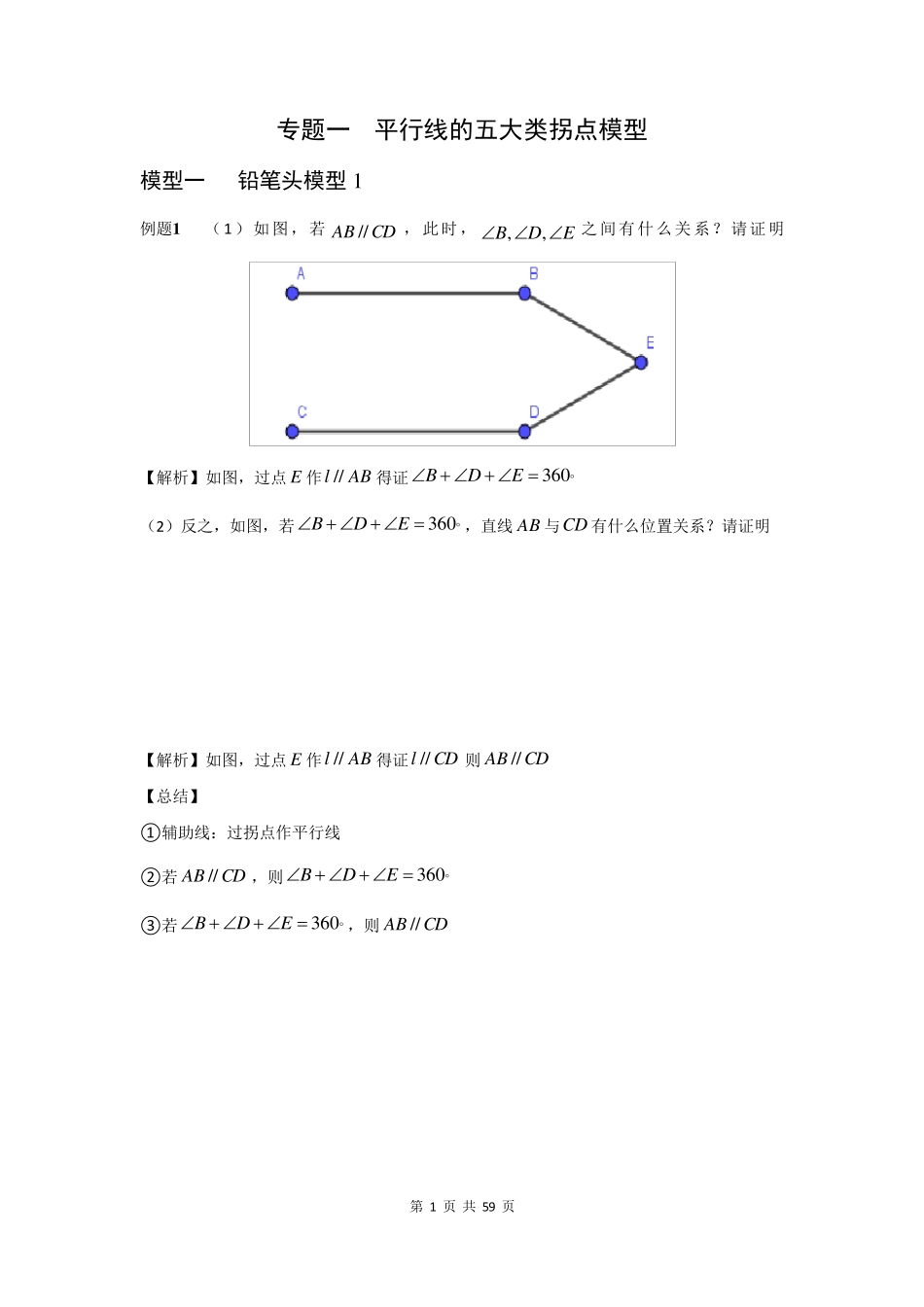
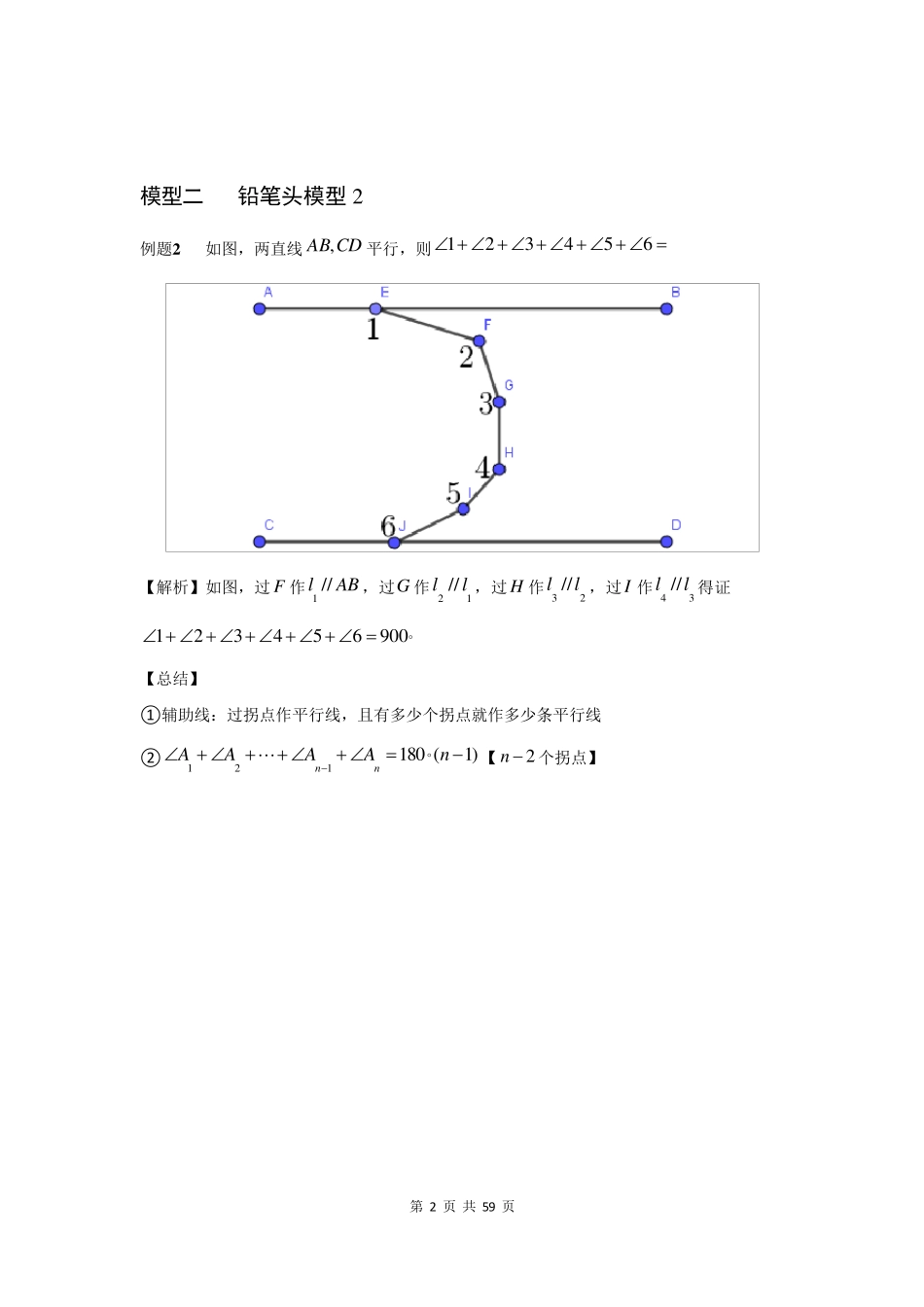
第 1 页 共 59 页 专题一 平行线的五大类拐点模型 模型一 铅笔头模型 1 例题1 （1）如图，若CDAB //，此时，EDB,,之间有什么关系？请证明 【解析】如图，过点 E 作ABl//得证3 6 0EDB （2）反之，如图，若3 6 0EDB，直线 AB 与CD 有什么位置关系？请证明 【解析】如图，过点 E 作ABl//得证CDl//则CDAB // 【总结】 ①辅助线：过拐点作平行线 ②若CDAB //，则3 6 0EDB ③若3 6 0EDB，则CDAB // 第 2 页 共 59 页 模型二 铅笔头模型2 例题2 如图，两直线CDAB,平行，则654321 【解析】如图，过 F 作ABl //1，过G 作12 //ll，过 H 作23 //ll，过I 作34 //ll得证 9 0 0654321 【总结】 ①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②)1(1 8 0121nAAAAnn【2n个拐点】 第 3 页 共 59 页 模型三 锯齿模型1 例题3 （1）如图，若CDAB //，则EDB，你能说明为什么吗？ 【解析】如图，过点 E 作ABl //得证EDB （2）在图中，CDAB //， GE与DFB又有何关系？ 【解析】如图，过点 E 作ABl //1，过点F 作ABl //2，过点G 作ABl //3得证 GE=DFB （3）在图中，若CDAB //，又得到什么结论？ 【解析】同理可得nnEEEDFFFB21121 【总结】 第 4 页 共 59 页 ①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和 模型四 锯齿模型2 例题4 如图所示，已知CDAB //，BE 平分ABC，DE 平分ADC，求证： )(21CAE 【解析】 ①方法一：锯齿模型【锯齿 ABEDC】如图，过点E 作ABEF //+转化思想得证 ②方法二：8 字模型（详解见第2 讲） 【总结】 ①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和 ③转化思想 例题5 如图，已知CDAB //，EABEAF41，ECDECF41，求证： AECAFC43 【解析】锯齿 BAECD+锯齿 BAFCD；过点E 作ABGE //，过点F 作CDHF //+方程思想【,表示角度】得证 【总结】 ①辅助线：过拐点作平行线，且有多少个拐点就作多...