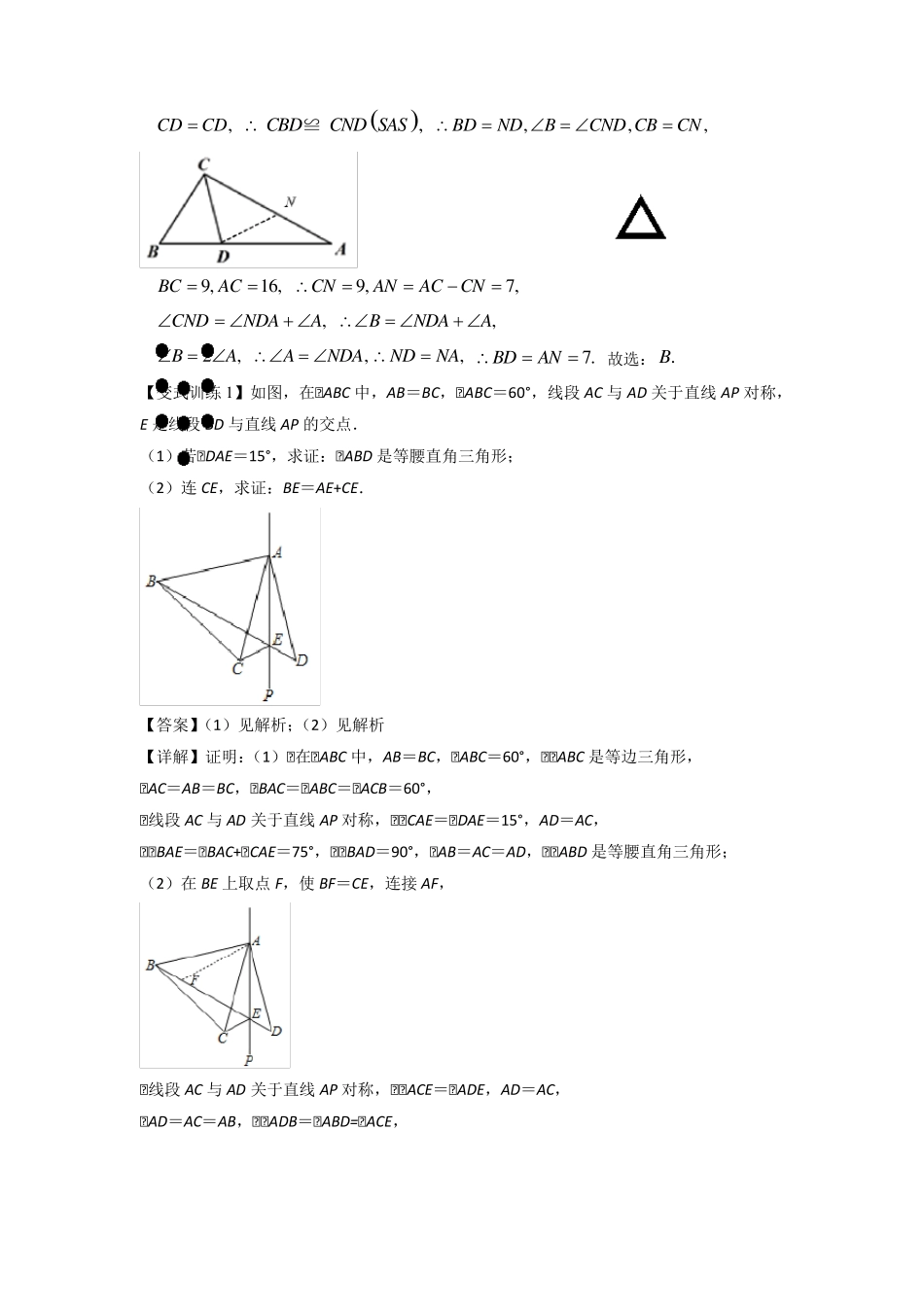
专题06 全等三角形的五种模型 全等三角形的模型种类多,其中有关中点的模型与垂直模型在前面的专题已经很详细的讲解,这里就不再重复。 模型一、截长补短模型 ①截长:在较长的线段上截取另外两条较短的线段。 如图所示,在BF上截取BM=DF,易证△BMC△△DFC(SAS),则 MC=FC=FG,△BCM=△DCF, 可得△MCF 为等腰直角三角形,又可证△CFE=45°,△CFG=90°, △CFG=△MCF,FG△CM,可得四边形CGFM 为平行四边形,则 CG=MF,于是BF=BM+MF=DF+CG. ②补短:选取两条较短线段中的一条进行延长,使得较短的两条线段共线并寻求解题突破。 如图所示,延长 GC 至 N,使 CN=DF,易证△CDF△△BCN(SAS), 可得 CF=FG=BN,△DFC=△BNC=135°, 又知△FGC=45°,可证 BN△FG,于是四边形BFGN 为平行四边形,得 BF=NG, 所以 BF=NG=NC+CG=DF+CG. 例 1.如图,△ABC 中,△B=2△A,△ACB 的平分线 CD 交 AB 于点D,已知 AC=16,BC=9,则 BD的长为( ) A.6 B.7 C.8 D.9 【答案】 .B 【详解】解:如图,在CA 上截取,CNCB 连接,DN CD 平分,ACB ,BCDNCD ,CDCD ,CBDCND SAS≌ ,,,BDNDBCND CBCN 9 ,1 6 ,BCAC 9 ,7 ,CNANACCN ,CNDNDAA ,BNDAA 2,BA ,ANDA ,NDNA 7 .BDAN 故选: .B 【变式训练 1】如图,在△ABC 中,AB=BC,△ABC=60°,线段 AC 与 AD 关于直线 AP 对称,E 是线段 BD 与直线 AP 的交点. (1)若△DAE=15°,求证:△ABD 是等腰直角三角形; (2)连 CE,求证:BE=AE+CE. 【答案】(1)见解析;(2)见解析 【详解】证明:(1)△在△ABC 中,AB=BC,△ABC=60°,△△ABC 是等边三角形, △AC=AB=BC,△BAC=△ABC=△ACB=60°, △线段 AC 与 AD 关于直线 AP 对称,△△CAE=△DAE=15°,AD=AC, △△BAE=△BAC+△CAE=75°,△△BAD=90°,△AB=AC=AD,△△ABD 是等腰直角三角形; (2)在 BE 上取点 F,使 BF=CE,连接 AF, △线段 AC 与 AD 关于直线 AP 对称,△△ACE=△ADE,AD=AC, △AD=AC=AB,△△ADB=△ABD=∠ACE, 在△ABF 与△ACE 中,ACABACEABFCEBF ,△△ABF△△ACE(SAS),△AF=AE, △AD=AB,△△D=△ABD,又△CAE=△DAE, △11...