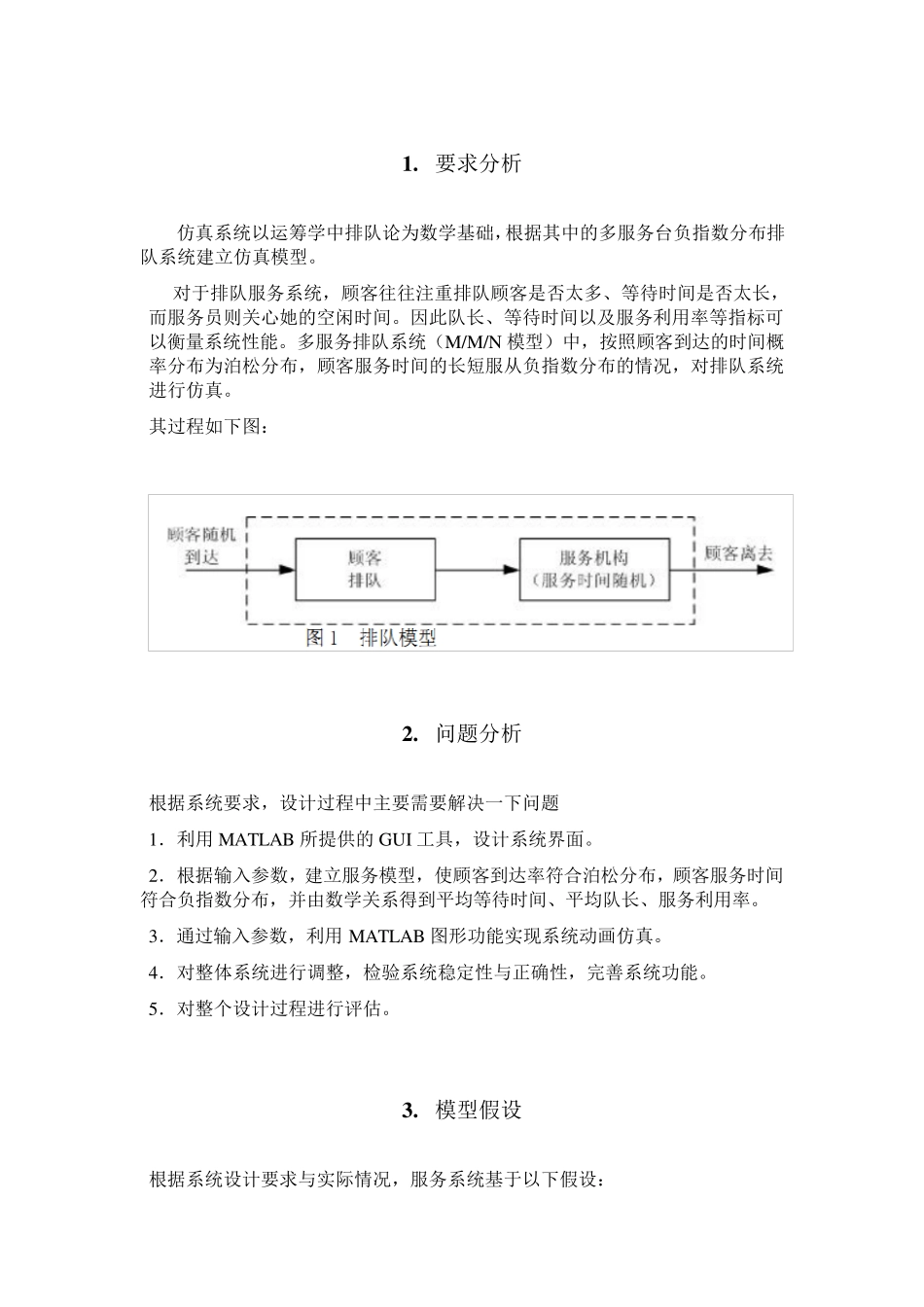
1 . 要求分析 仿真系统以运筹学中排队论为数学基础,根据其中的多服务台负指数分布排队系统建立仿真模型。 对于排队服务系统,顾客往往注重排队顾客是否太多、等待时间是否太长,而服务员则关心她的空闲时间。因此队长、等待时间以及服务利用率等指标可以衡量系统性能。多服务排队系统(M/M/N 模型)中,按照顾客到达的时间概率分布为泊松分布,顾客服务时间的长短服从负指数分布的情况,对排队系统进行仿真。 其过程如下图: 2 . 问题分析 根据系统要求,设计过程中主要需要解决一下问题 1.利用 MATLAB 所提供的GUI 工具,设计系统界面。 2.根据输入参数,建立服务模型,使顾客到达率符合泊松分布,顾客服务时间符合负指数分布,并由数学关系得到平均等待时间、平均队长、服务利用率。 3.通过输入参数,利用 MATLAB 图形功能实现系统动画仿真。 4.对整体系统进行调整,检验系统稳定性与正确性,完善系统功能。 5.对整个设计过程进行评估。 3 . 模型假设 根据系统设计要求与实际情况,服务系统基于以下假设: 1 1 .顾客源是无穷的; 2 .排队长度没有限制; 3 .到达系统的顾客按先到先服务原则依次进入服务; 4 .服务员在仿真过程中没有休假; 5 .顾客到达时排成一队,当有服务台空闲时进入服务状态; 6 .单位时间内到达的顾客数量服从泊松分布; 7 .顾客所需的服务时间服从负指数分布; 8 .各服务台服务无相互影响且平均服务时间相同。 4 . 模型分析 4.1 排队系统构成 系统设计过程中,将排队过程分为到达过程,排队过程,服务过程三部分。 4.1.1 到达过程 到达过程主要针对顾客到达情况,对于不同的模型背景,顾客到达情况有不同的限制,此次系统设计过程中顾客到达基于以下假设: 1. 顾客源是无限的。 2. 顾客单个到来,且相互独立。 3. 顾客到达的时间服从泊松分布,且到达过程是平稳的。 4.1.2 排队过程 排队过程规定顾客在排队过程中的排队规则,即规定顾客在排队系统中按怎样的规则、次序接收服务的,本次系统设计采用以下排队规则: 1. 顾客到达时若所有服务台均被占用,则顾客均选择排队等候。 2. 顾客的服务次序采取先到先服务。 3. 队列数目为单列,顾客不会在排队过程中中途退出。 2 4.1.3 服务过程 服务过程规定顾客在接收服务过程中的服务规则,本次系统设计采用一下服务规则: 1. 服务机构为多服务台并联型(包括单服务台的特殊情况),各服务...