matlab传染病模型VIP免费

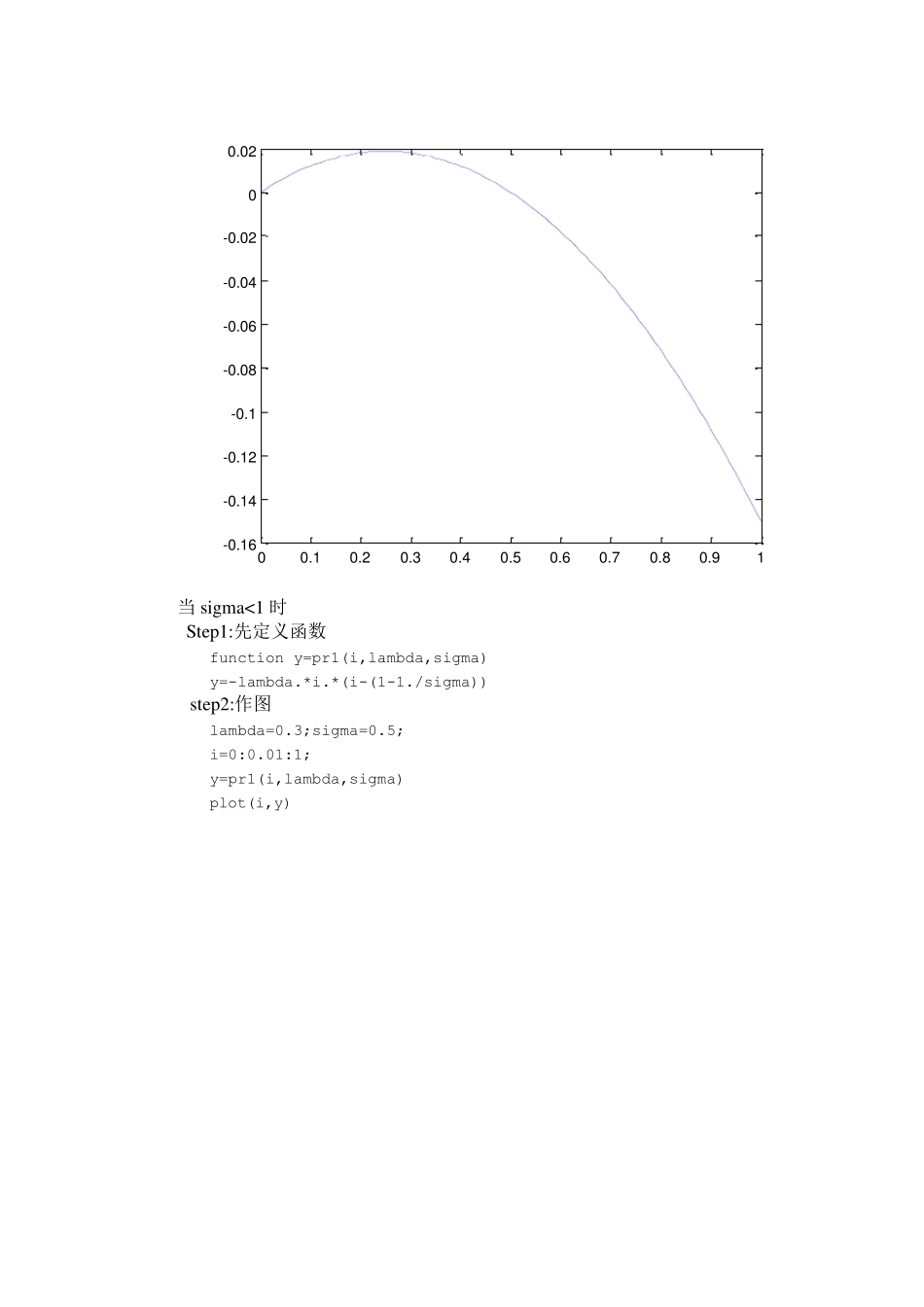
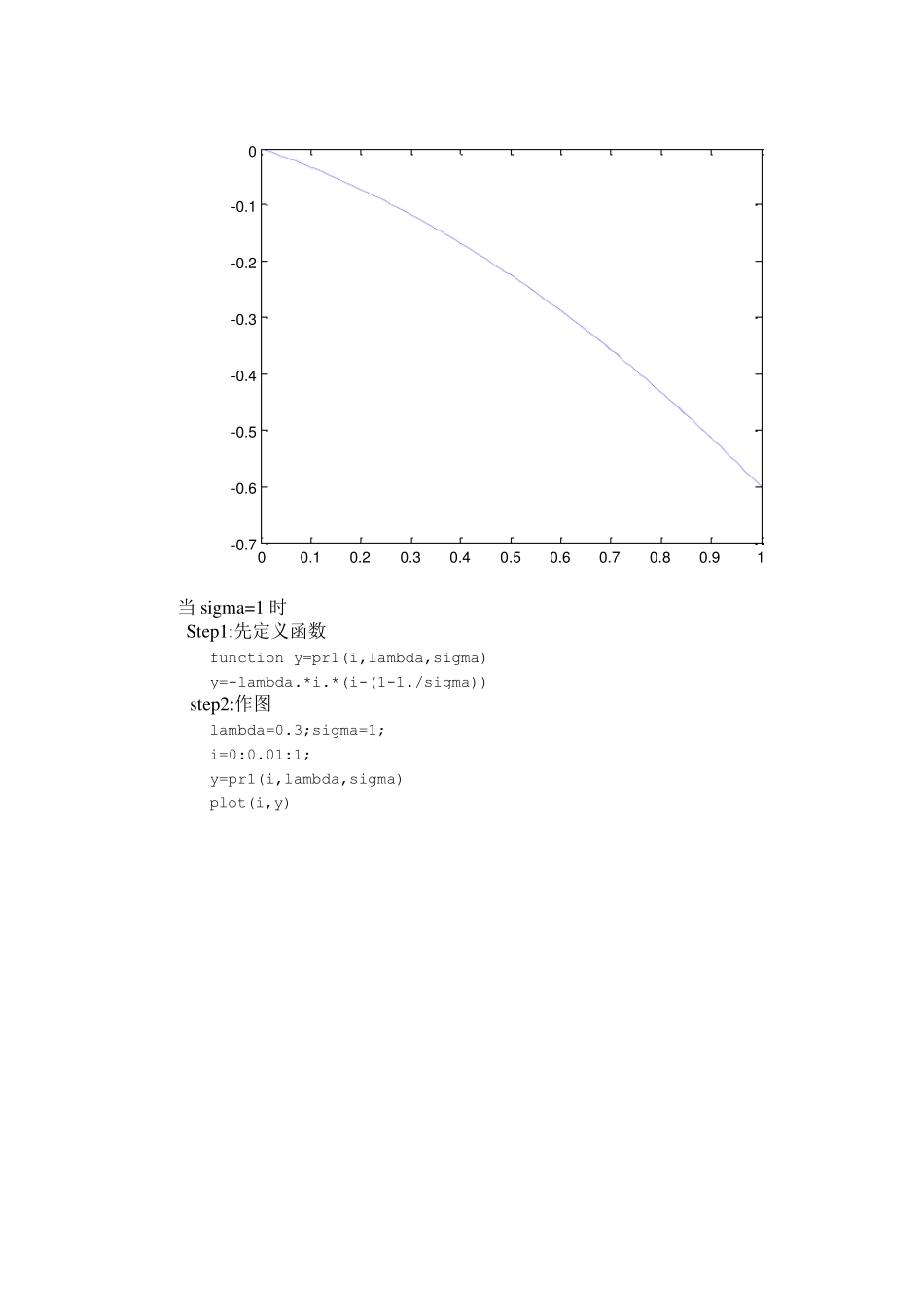
传染病模型实验 实验目的： 理解传染病的四类模型，学会利用Matlab 软件求解微分方程（组）。 实验题目： 利用Matlab 求解传染病的SIS 微分方程模型，并绘制教材P139 页图3-图6。 S IS 模型 假设： (1)、 t时刻人群分为易感者(占总人数比例的s(t))和已感染者(占总人数比例的i(t))。 (2)、 每个病人每天有效接触的平均人数是常数 ， 称为日接触率，当健康者与病人接触时，健康者受感染成为病人。 (3)、病人每天被治愈的占病人总数的比例为  ，称为日治愈率，显然 1 为这种传染病的平均传染期。 则建立微分方程模型为： 令，则模型可写作 分别作图： 当 sigma>1 时 Step1:先定义函数 function y=pr1(i,lambda,sigma) y=-lambda.*i.*(i-(1-1./sigma)) step2:作图 lambda=0.3;sigma=2; i=0:0.01:1; y=pr1(i,lambda,sigma) plot(i,y) 00 .10 .20 .30 .40 .50 .60 .70 .80 .91-0 .1 6-0 .1 4-0 .1 2-0 .1-0 .0 8-0 .0 6-0 .0 4-0 .0 200 .0 2 当sigma<1 时 Step1:先定义函数 function y=pr1(i,lambda,sigma) y=-lambda.*i.*(i-(1-1./sigma)) step2:作图 lambda=0.3;sigma=0.5; i=0:0.01:1; y=pr1(i,lambda,sigma) plot(i,y) 00 .10 .20 .30 .40 .50 .60 .70 .80 .91-0 .7-0 .6-0 .5-0 .4-0 .3-0 .2-0 .10 当sigma=1 时 Step1:先定义函数 function y=pr1(i,lambda,sigma) y=-lambda.*i.*(i-(1-1./sigma)) step2:作图 lambda=0.3;sigma=1; i=0:0.01:1; y=pr1(i,lambda,sigma) plot(i,y) 00 .10 .20 .30 .40 .50 .60 .70 .80 .91-0 .3 5-0 .3-0 .2 5-0 .2-0 .1 5-0 .1-0 .0 50 当sigma>1 时 Step1:先定义函数 function di=crb(t,i,lambda,sigma) di=-lambda*i*(i-(1-1/sigma)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% step2:求解并作图 clc clear lambda=0.01; sigma=2; [t,i1]=ode45(@crb,[0,1000],0.9,[],lambda,sigma); [t,i2]=ode45(@crb,[0,1000],0.2,[],lambda,sigma); plot(t,i1,t,i2,t,1/2) legend('\sigma>1') 010020030040050060070080090010000.20.30.40.50.60.70.80.91>1 当sigma=1 时 Step1:先定义函数 function di=crb(t,i,lambda,sigma) di=-lambda*i*(i-(1-1/sigma)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% step2:求解并作图 clc clear lambda=0.01; sigma=1...