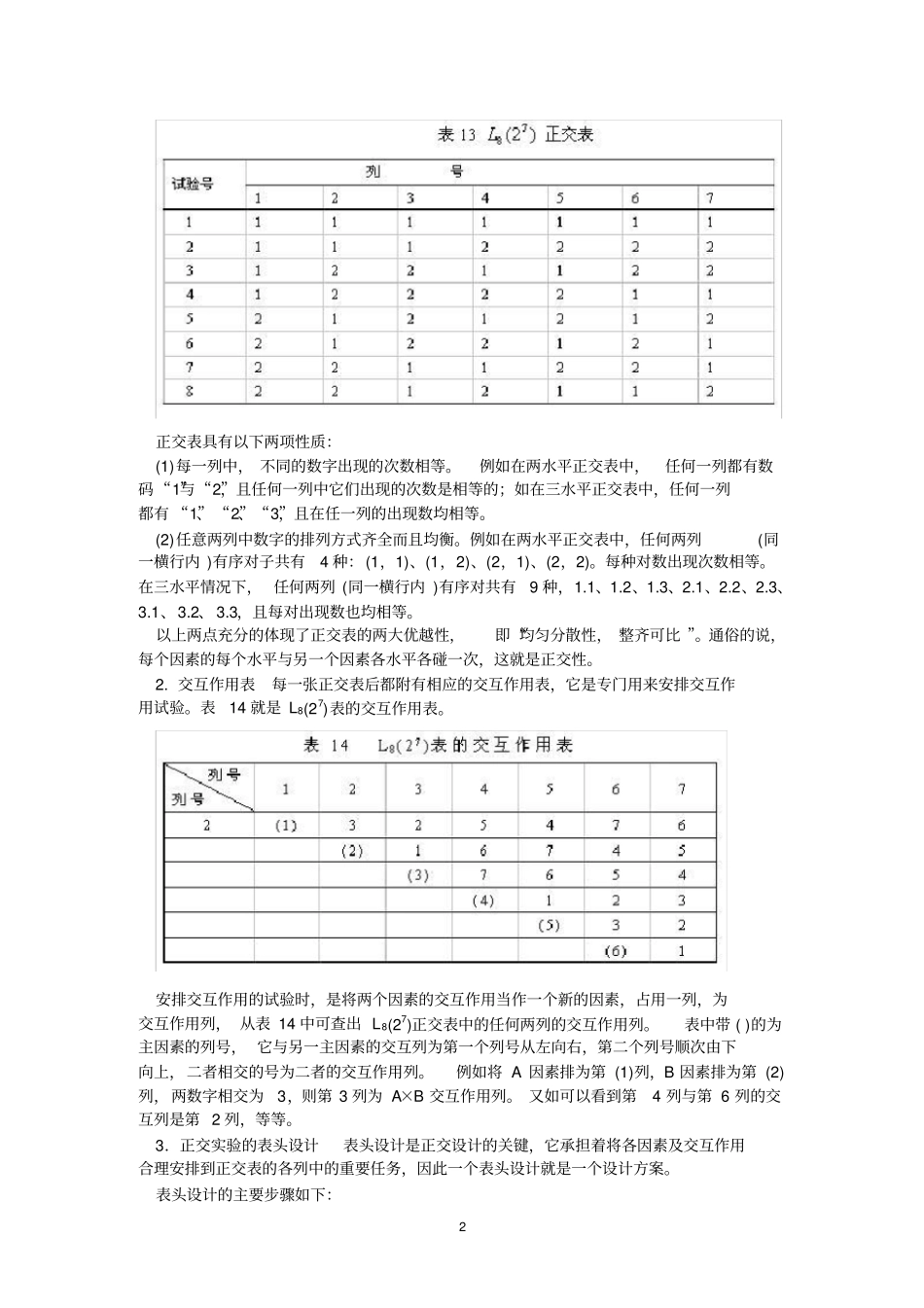
1 正交实验设计当析因设计要求的实验次数太多时,一个非常自然的想法就是从析因设计的水平组合中, 选择一部分有代表性水平组合进行试验。因此就出现了分式析因设计(fractional factorial designs),但是对于试验设计知识较少的实际工作者来说,选择适当的分式析因设计还是比较困难的。正交试验设计 (Orthogonal experimental design) 是研究多因素多水平的又一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了 “均匀分散,齐整可比”的特点,正交试验设计是分式析因设计的主要方法。是一种高效率、快速、经济的实验设计方法。日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格,称为正交表。例如作一个三因素三水平的实验,按全面实验要求,须进行33=27 种组合的实验,且尚未考虑每一组合的重复数。若按L9(3)3 正交表按排实验,只需作9 次,按 L18(3)7 正交表进行18 次实验,显然大大减少了工作量。因而正交实验设计在很多领域的研究中已经得到广泛应用。 1.正交表正交表是一整套规则的设计表格,用。L 为正交表的代号, n 为试验的次数,t 为水平数, c 为列数,也就是可能安排最多的因素个数。例如L 9(34), (表 11),它表示需作 9 次实验,最多可观察4 个因素,每个因素均为3 水平。一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4 ×24) (表 12),此表的 5 列中,有 1列为 4 水平,4 列为 2 水平。根据正交表的数据结构看出,正交表是一个n 行 c 列的表,其中第 j 列由数码 1,2,⋯ Sj 组成,这些数码均各出现N/S 次,例如表 11 中,第二列的数码个数为3,S=3 ,即由 1、2、 3 组成,各数码均出现次。2 正交表具有以下两项性质: (1)每一列中, 不同的数字出现的次数相等。例如在两水平正交表中,任何一列都有数码“1”与“2”,且任何一列中它们出现的次数是相等的;如在三水平正交表中,任何一列都有 “1”、 “2”、“3”,且在任一列的出现数均相等。 (2)任意两列中数字的排列方式齐全而且均衡。例如在两水平正交表中,任何两列(同一横行内 )有序对子共有4 种:(1,1)、(1,2)、(2,1)、(2,2)。每种对数出现次数相等。在三水平情况下, 任何两列 (同一横行内 )有序对共有9 种,1.1、1.2、1.3、2.1、2.2、2.3、3.1、3.2、 3.3,且每对出现数也均相等。以上两点充分的体现了正...