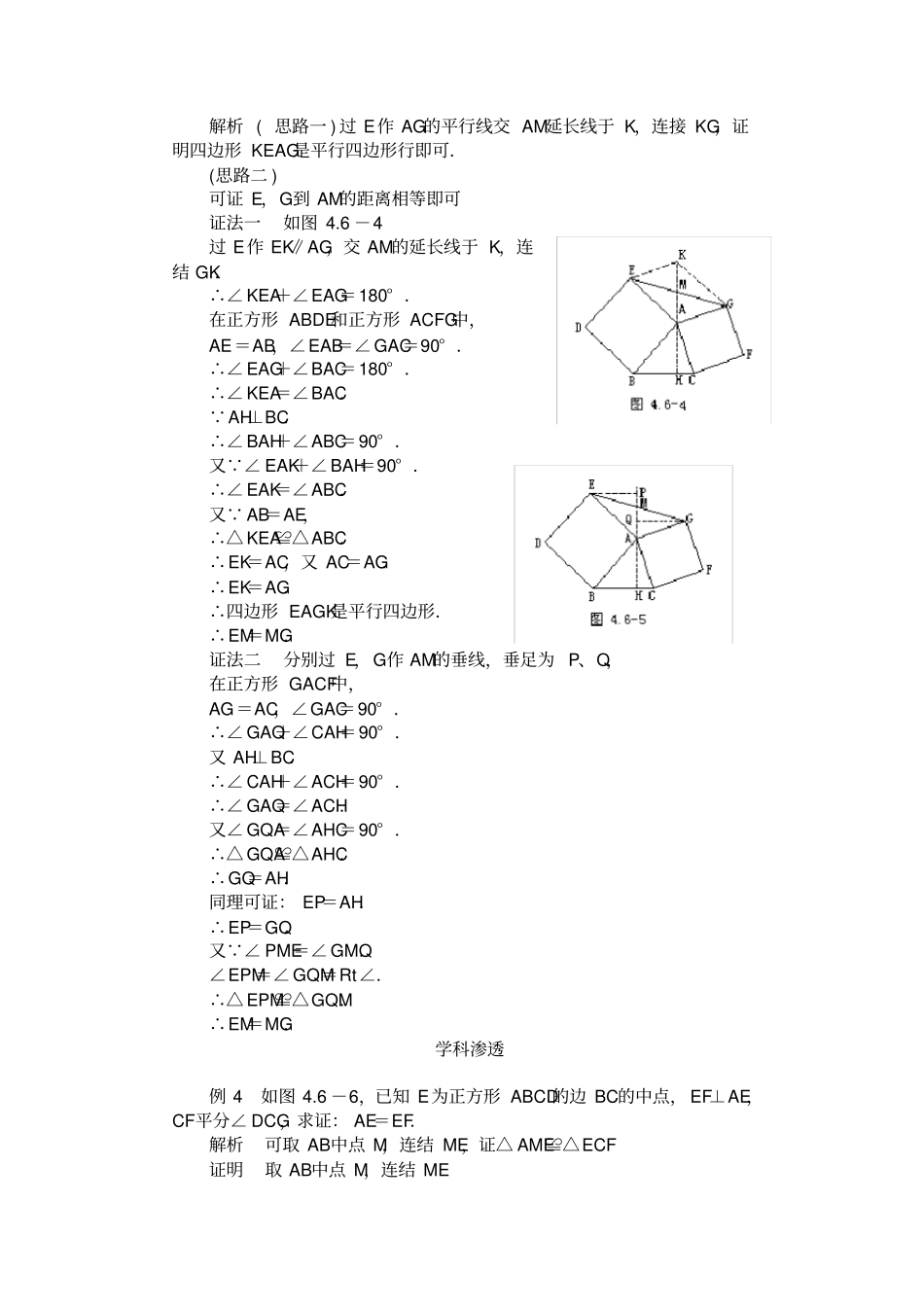
正方形· 典型例题能力素质例 1 如图 4.6 -2,已知正方形 ABCD中,E 为 AD上一点, BF平分∠ EBC交 DC于 F,求证: BE=AE+CF.解析证 AE+CF=BE,可以把 AE与 CF相接,证其与 BE相等.证明延长 EA到 G,使 AG=CF,连结 BG.在正方形 ABCD中,AB =BC,∠BAG=∠ C=90° .∴△ GAB≌△FCB.∴∠ GBA=∠FBC.∠G=∠ BFC.又 AB∥CD.∴∠ BFC=∠ABF=∠ EBA+∠ EBF.又 BF平分∠ EBC,∴∠ EBF=∠FBC.∴∠ GBA=∠EBF.∴∠ G=∠ BFC=∠ EBA+∠EBF =∠ EBA+∠GBA =∠ EBG.∴BE=GE=AG+AE=CF+AE.点击思维例 2 如图 4.6 -3,已知锐角△ ABC中,以 AB,AC为边向外作正方形 ABDE和正方形 ACFG,连结 CE、BG,交点为 O,求证:(1)EC=BG;(2)EC⊥BG.解析易证△ EAC≌△ BAG,可得 EC=BG,∠AEC=∠ ABG,于是可证∠EOB=∠EAB 证明 (1)在正方形 ABDE和正方形 ACFG中,AE=AB,AC=AG,∠EAB=∠ GAC=90° ,∴∠ EAB+∠BAC=∠ GAC+∠ BAC.即∠ EAC=∠BAG,∴△ EAC≌△BAG.∴EC=BG.(2)由(1) 知:△ EAC≌△ BAG,∴∠ AEC=∠ABG.又 ∠ 1=∠2,∴∠ ABG+∠2=∠ AEC+∠1=90° .∴∠ EOB=∠EAB=90° ∴ EC⊥BG.点评若把例题中,∠ BAC为锐角改为钝角,其余条件不变,上述两结论仍能成吗?如果成立试证明之.例 3 如图 4.6 -4,以△ABC的边 AB,AC为边向形外作正方形ABDE和正方形 ACFG,AH⊥BC,交 EG于 M,垂足为 H,求证: EM=MG.解析 ( 思路一 ) 过 E作 AG的平行线交 AM延长线于 K,连接 KG,证明四边形 KEAG是平行四边形行即可.(思路二 ) 可证 E,G到 AM的距离相等即可证法一如图 4.6 -4 过 E作 EK∥AG,交 AM的延长线于 K,连结 GK.∴∠ KEA+∠EAG=180° .在正方形 ABDE和正方形 ACFG中,AE=AB,∠EAB=∠ GAC=90° .∴∠ EAG+∠BAC=180° .∴∠ KEA=∠BAC. AH⊥BC.∴∠ BAH+∠ABC=90° .又 ∠ EAK+∠ BAH=90° .∴∠ EAK=∠ABC.又 AB=AE,∴△ KEA≌△ABC.∴EK=AC,又 AC=AG.∴EK=AG.∴四边形 EAGK是平行四边形.∴EM=MG.证法二分别过 E,G作 AM的垂线,垂足为 P、Q,在正方形 GACF中,AG=AC,∠GAC=90° .∴∠ GAQ+∠CAH=90° .又 AH⊥BC.∴∠ CAH+∠ACH=90° .∴∠ GAQ=∠ACH.又∠ GQA...