常见的概率分布VIP免费

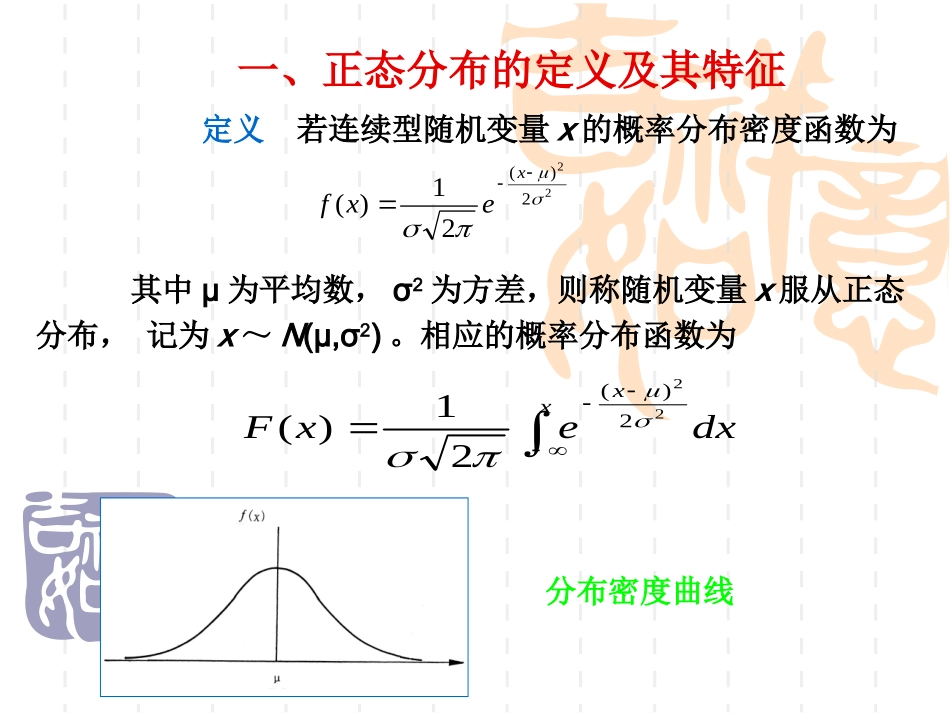
常见的概率分布正态分布二项分布波松分布三种概率分布的关系正态分布壹.正态分布的定义及其特征贰.标准正态分布叁.正态分布的概率计算.肆.伍1.标准正态分布的概率计算.陆.柒2.一般正态分布的概率计算一、正态分布的定义及其特征定义若连续型随机变量x的概率分布密度函数为其中μ为平均数，σ2为方差，则称随机变量x服从正态分布，记为x～N(μ,σ2)。相应的概率分布函数为222)(21)(xexfxxdxexF222)(21)(分布密度曲线正态分布的特征1、正态分布密度曲线是单峰、对称的悬钟形曲线，对称轴为x=μ；2、f(x)在x=μ处达到极大，极大值；3、f(x)是非负函数，以x轴为渐近线，分布从-∞至+∞；4、曲线在x=μ±σ处各有一个拐点，即曲线在(-∞,μ-σ)和(μ+σ,+∞)区间上是下凸的，在[μ-σ,μ+σ]区间内是上凸的；5、正态分布有两个参数，即平均数μ和标准差σ。【μ是位置参数，如图所示。当σ恒定时，μ愈大，则曲线沿x轴愈向右移动；反之，μ愈小，曲线沿x轴愈向左移动。σ是变异度参数，如图所示。当μ恒定时，σ愈大，表示x的取值愈分散，曲线愈“胖”；σ愈小，x的取值愈集中在μ附近，曲线愈“瘦”。】6、分布密度曲线与横轴所夹的面积为1，即：21)(f121)(222)(dxexPx二、标准正态分布定义：μ=0,σ2=1的正态分布，记作X～N(0，1)。【用Z代替X】概率密度函数分布函数概率密度函数图对于任何一个服从正态分布N(μ,σ2)的随机变量x，都可以通过标准化变换：Z=(x-μ)／σ将其变换为服从标准正态分布的随机变量z。Z称为标准正态变量或标准正态离差.三、正态分布的概率计算1、标准正态分布的概率计算设Z服从标准正态分布，则Z在[z1,z2）内取值的概率为：＝Φ(Z2)－Φ(Z1)而Φ(Z1)与Φ(Z2)可由附表查得。（2）一般正态分布的概率计算X~N(μ,σ2)，则x的取值落在任意区间[x1,x2）的概率P(x1≤x＜x2)的计算。参数转换：【】阴影部分曲边梯形面积双侧概率(两尾概率):我们把随机变量x落在平均数μ加减不同倍数标准差σ区间之外的概率称为记作α。单侧概率(一尾概率),:对应于双侧概率可以求得随机变量x小于μ-kσ或大于μ+kσ的概率，称为记作α／2。【例】x落在(μ-1.96σ,μ+1.96σ)之外的双侧概率为0.05，而单侧概率为0.025。P(x＜μ-1.96σ)=P(x＞μ+1.96σ)=0.025x落在(μ-2.58σ,μ+2.58σ)之外的双侧概率为0.01，而单侧概率为0.005。P(x＜μ-2.58σ)=P(x＞μ+2.58σ)=0.005