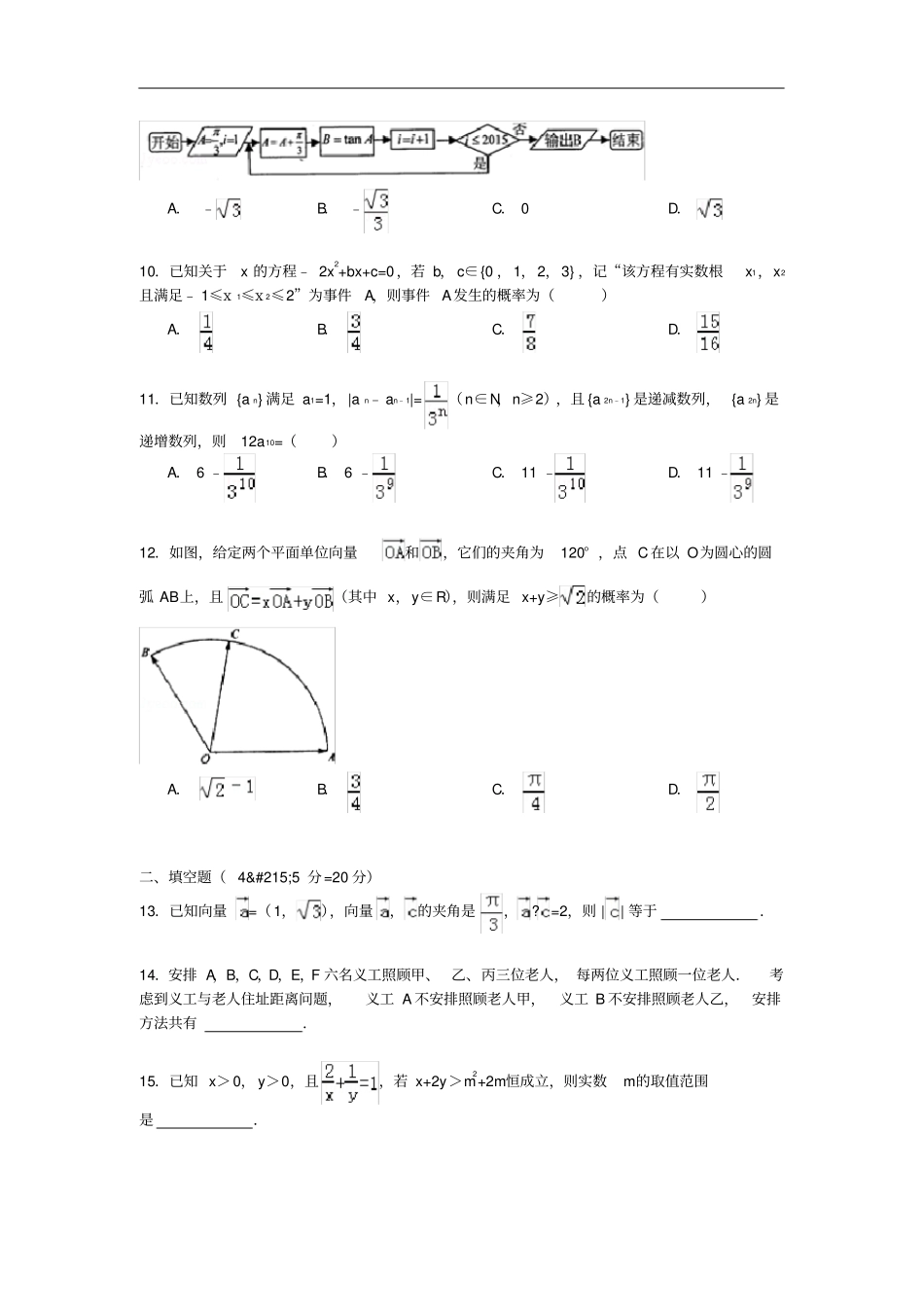
江西省南昌二中2014-201 5 学年高一(下)期末数学试卷一、选择题( 12×5 分=60 分)1.下列函数中,最小正周期为的是()A.B.C. D.2.把函数 y=sin ( 2x﹣)的图象向右平移个单位,再向下平移2 个单位所得函数的解析式为()A. y=cos2x ﹣2 B. y= ﹣cos2x ﹣2 C. y=sin2x ﹣ 2 D. y= ﹣cos2x+2 3.某校现有高一学生210 人,高二学生270 人,高三学生300 人,用分层抽样的方法从这三个年级的学生中随机抽取n 名学生进行问卷调查, 如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数为()A. 7 B. 8 C. 9 D. 10 4.等差数列 {a n} 的公差 d≠0, a1=20,且 a3,a7,a9成等比数列. Sn为{a n} 的前 n 项和,则S10 的值为()A. ﹣110 B. ﹣90 C. 90 D. 110 5.已知向量、的夹角为 60° ,,若,则=()A.B.C.D.6.甲、乙两人各自在300 米长的直线形跑道上跑步,则在任一时刻两人在跑道相距不超过50 米的概率是()A.B.C.D.7.甲、乙两人从4 门课程中各选修2 门,则甲、乙所选的课程中至少有1 门不相同的概率等于()A.B.C.D.8.若关于 x 的不等式 x2+ax﹣2>0 在区间 [1 , 5] 上有解,则实数a 的取值范围为()A. (﹣,+∞) B. [ ﹣,1] C. ( 1,+∞)D.(﹣∞,﹣ 1)9.下列程序图中,输出的B 是()A. ﹣B. ﹣C. 0 D.10.已知关于x 的方程﹣ 2x2+bx+c=0,若 b, c∈{0 ,1,2,3} ,记“该方程有实数根x1,x2且满足﹣ 1≤x 1≤x 2≤2”为事件A,则事件 A发生的概率为()A.B.C.D.11.已知数列 {a n} 满足 a1=1,|a n﹣ an﹣1|=(n∈N,n≥2),且 {a 2n﹣1} 是递减数列, {a 2n} 是递增数列,则12a10=()A. 6 ﹣B. 6 ﹣C. 11 ﹣D. 11 ﹣12.如图,给定两个平面单位向量和,它们的夹角为120° ,点 C在以 O为圆心的圆弧 AB上,且(其中 x,y∈R),则满足 x+y≥的概率为()A.B.C.D.二、填空题( 4×5 分=20 分)13.已知向量=(1,),向量,的夹角是,? =2,则 || 等于.14.安排 A,B,C,D,E,F 六名义工照顾甲、 乙、丙三位老人, 每两位义工照顾一位老人.考虑到义工与老人住址距离问题,义工 A 不安排照顾老人甲,义工 B 不安排照顾老人乙,安排方法共有.15.已知 x>0, y>0,且,若 x+2y>m2+2m恒成立,...