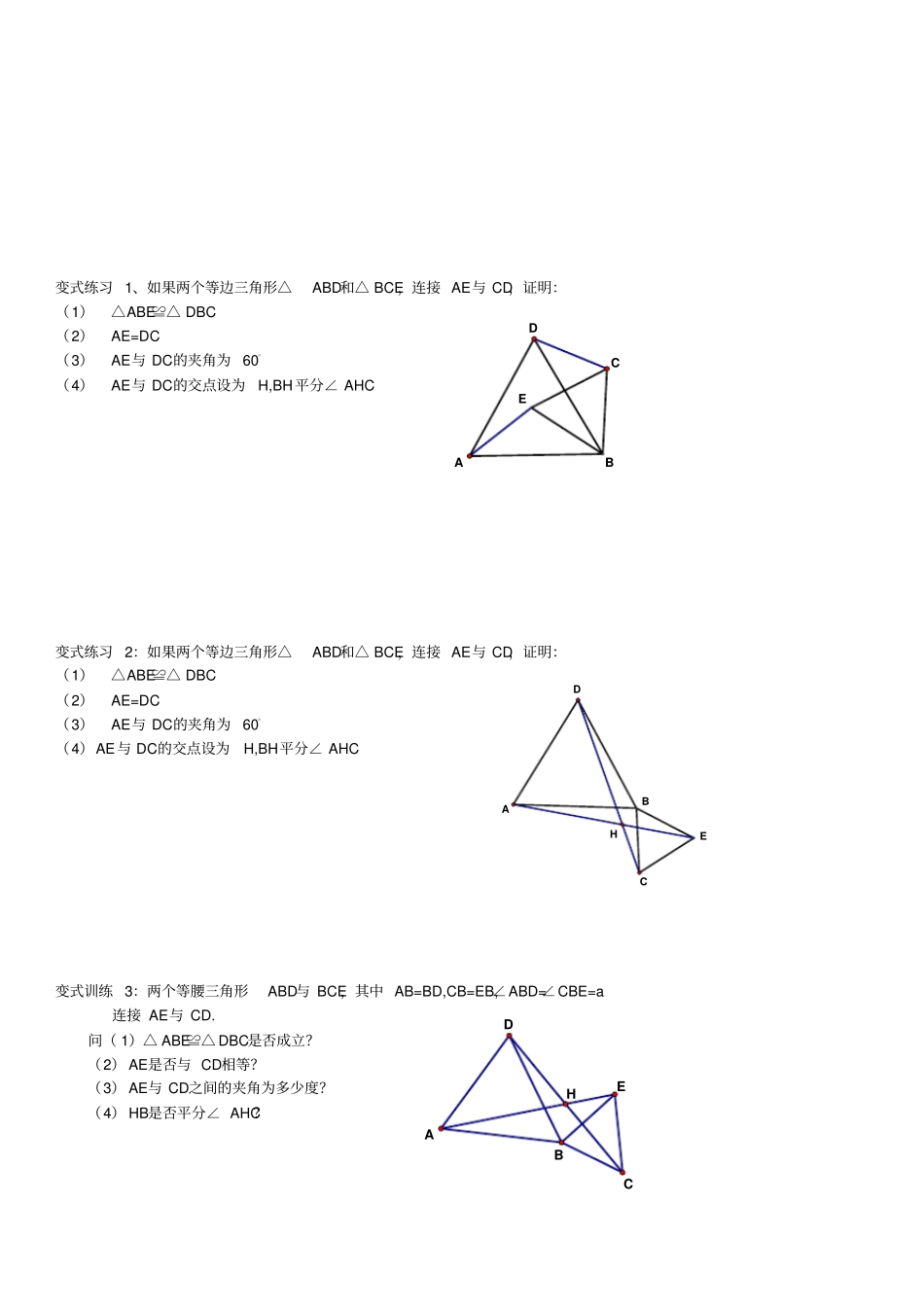
一、手拉手模型:1 手的判别:判断左右,将等腰三角形顶角顶点朝上,左边为左手顶点,右边为右手顶点。2 手拉手的定义两个顶角相等且有共顶点的等腰三角形形成的图形。(左手拉左手,右手拉右手)3 手拉手基本结论①△ ABC≌△ AB'C'(SAS) ②∠ BAB'=∠BOB' ③AO平分∠ BOC' 二、例题例 1、在直线 ABC的同一侧作两个等边三角形△ABD和△ BCE,连接 AE与 CD,证明:(1)△ABE≌△ DBC (2)AE=DC (3)AE与 DC的夹角为 60。(4)△AGB≌△ DFB (5)△EGB≌△ CFB (6)BH平分∠ AHC (7)GF∥ AC HFGEDABC变式练习 1、如果两个等边三角形△ABD和△ BCE,连接 AE与 CD,证明:(1)△ABE≌△ DBC (2)AE=DC (3)AE与 DC的夹角为 60。(4)AE与 DC的交点设为H,BH平分∠ AHC 变式练习 2:如果两个等边三角形△ABD和△ BCE,连接 AE与 CD,证明:(1)△ABE≌△ DBC (2)AE=DC (3)AE与 DC的夹角为 60。(4)AE与 DC的交点设为H,BH平分∠ AHC 变式训练 3:两个等腰三角形ABD与 BCE,其中 AB=BD,CB=EB,∠ABD=∠CBE=a 连接 AE与 CD. 问( 1)△ ABE≌△ DBC是否成立?(2) AE是否与 CD相等?(3) AE与 CD之间的夹角为多少度?(4) HB是否平分∠ AHC?EBDACHEBDACHDABCE例 2:如图,两个正方形ABCD和 DEFG,连接 AG与 CE,二者相交于H 问:(1)△ ADG≌△ CDE是否成立?(2) AG是否与 CE相等?(3) AG与 CE之间的夹角为多少度?(4) HD是否平分∠ AHE?例 3:如图两个等腰直角三角形ADC与 EDG,连接 AG,CE,二者相交于H. 问 (1)△ ADG≌△ CDE是否成立?(2) AG是否与 CE相等?(3) AG与 CE之间的夹角为多少度?(4) HD是否平分∠ AHE?二、半角模型1、条件:2、思路:①截长补短②旋转例 1、在正方形ABCD中,若 M、N分别在边 BC、CD上移动,且满足MN=BM +DN,求证:① . ∠MAN=②.③. AM、AN分别平分 ∠BMN和∠DNM. .180210且45ABCCMN2HEFADBCGHGADCE例 2 拓展:在正方形ABCD中,已知∠ MAN=,若 M、N分别在边 CB、DC的延长线上移动,①. 试探究线段MN、BM 、DN之间的数量关系. ②. 求证: AB=AH. 例 3. 在四边形 ABCD中,∠ B+∠D=,AB=AD,若 E、F 分别在边 BC、CD上,且满足EF=BE +DF. 求证:练习巩固1:(1)如图 1,在正方形ABCD中, E、F 分别是 BC、 CD上的点,且∠ EAF=45° ,试判断BE、...