空间角大小比较VIP免费

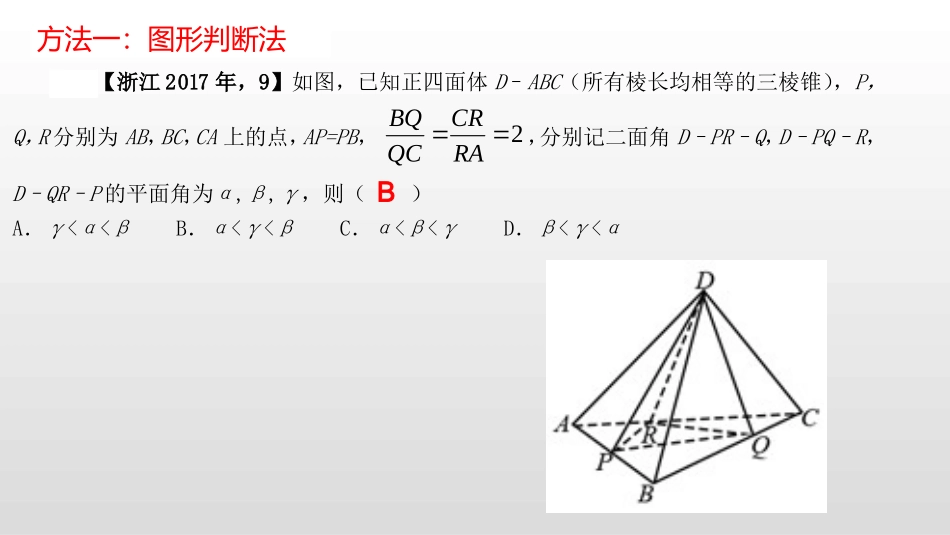
空间角大小比较在此输入您的封面副标题例4【浙江2017年，9】如图，已知正四面体D–ABC（所有棱长均相等的三棱锥），P，Q，R分别为AB，BC，CA上的点，AP=PB，2BQCRQCRA，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α,β,γ，则（）A．γ<α<βB．α<γ<βC．α<β<γD．β<γ<αB方法一：图形判断法....DCBACMDPCABPCMNPADNABMABCDP），则（，，为，，中点，分别记二面角的是点（不包括端点），上的动是的各棱长均相等，如图，已知正四棱锥PANMBCDD(2015浙江）.如图，已知ABC，D是AB的中点，沿直线CD将ACD折成ACD，所成二面角ACDB的平面角为，则（）A.ADBB.ADBC.ACBD.CBA'B方法二、极端位置分析法方法三：最小角原理和最大角原理线线角≧线面角线面角≦面面角线面角最小二面角最大锐二面角练习1.如图所示，已知三棱锥DABC，记二面角CABD的平面角是，直线DA与平面ABC所成的角是1，直线DA与BC所成角是2，则（）A．1B.1C.2D.2A2.如图所示，在侧棱垂直于底面的三棱柱111ABCABC，P棱BC上的动点，记直线1AP与平面ABC所成角为1，与BC所成角是2，则1，2的大小关系是（）A．12B.12C.12D.不能确定C例2【浙江2019年，8】设三棱锥VABC的底面是正三角形，侧棱长均相等，P是棱VA上的点（不含端点），记直线PB与直线AC所成角为，直线PB与平面ABC所成角为，二面角PACB的平面角为，则（）A.,B.,C.,D.,B）方法：由最小角定理，记的平面角为（显然，由最大角定理1例2【浙江2018年，8】已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S−AB−C的平面角为θ3，则（）A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1D例3、(2014浙江）如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若AB=15m，AC=25m，∠BCM=30∘，则tanθ的最大值是________．（仰角θ为直线AP与平面ABC所成角）935练习.如图所示，已知三棱锥ABCD的所有棱长均相等，点E满足3DEEC�，点P在棱AC上运动，设EP与平面BCD所成角为，则sin的最大值是.