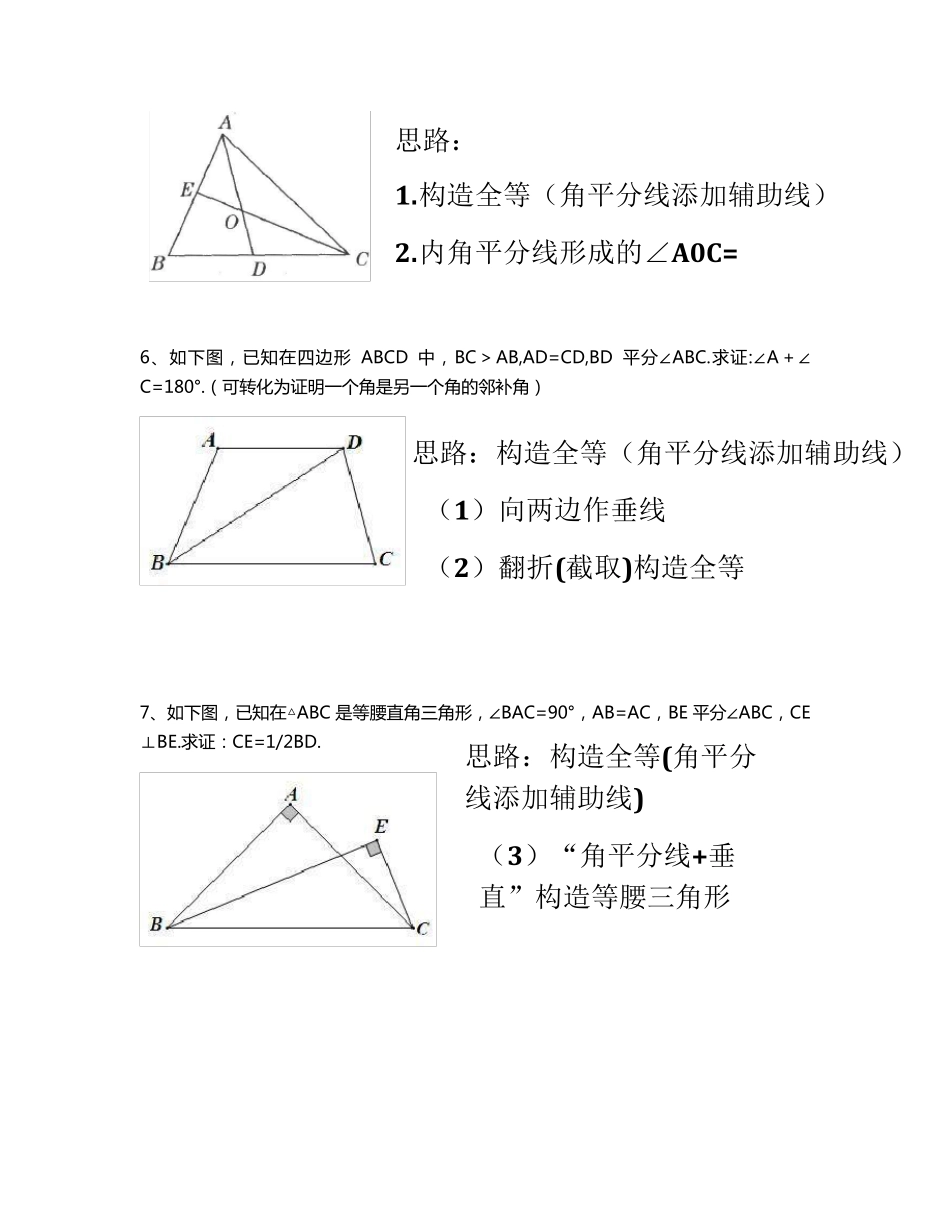
人 教 版 八 年 级 数 学 上 册 全 等 三角形 典型 6 类难题题型归类 一、角平分线型 角平分线是轴对称图形,所以我们要充分的利用它的轴对称性,常作的辅助线是:一利用截取一条线段构造全等三角形,二是经过平分线上一点作两边的垂线 。 (1)构造全 等 三角形 1. 如图,在Δ ABC 中, D 是边 BC 上一点, AD 平分∠ BAC ,在 AB 上截取 AE=AC ,连结 DE ,已知 DE=2cm , BD=3cm ,求线段 BC 的长。 2. 已知:如图所示, BD 为∠ ABC 的平分线, AB=BC ,点 P 在 BD 上, PM ⊥ AD 于 M , •PN ⊥ CD 于 N ,判 断 PM 与 PN 的关 系 . PDACBMN思路:截取构造全等三角形 思路:构造全等三角形 3. 已 知 : 如 图 E 在 △ ABC 的 边 AC 上 , 且 ∠ AEB= ∠ ABC 。 (1) 求 证 : ∠ ABE= ∠ C ; (2) 若 ∠ BAE 的 平 分 线 AF 交 BE 于 F , FD ∥ BC 交 AC 于 D , 设 AB=5 , AC=8 ,求 DC 的 长 。 4、 如 图 所 示 , 已 知 ∠ 1= ∠ 2 , EF ⊥ AD 于 P , 交 BC 延 长 线 于 M , 求 证 : 2 ∠ M= ( ∠ ACB- ∠ B ) 5、 如 图 , 在 △ ABC 中 , ∠ ABC=60 °, AD 、 CE 分 别 平 分 ∠ BAC 、∠ ACB , 求 证 : AC=AE+CD . 21PFMDBACE思路: 外角的性质+代数思想 思路: (1)三角形内角和+等量代换 (2)构造全等三角形 6、如 下 图 , 已 知 在 四 边 形ABCD 中 , BC> AB,AD=CD,BD 平 分 ∠ABC.求 证 :∠A+ ∠C=180°.( 可 转 化 为 证 明 一 个 角 是 另 一 个 角 的 邻 补 角 ) 7、如 下 图 , 已 知 在 △ABC 是 等 腰 直 角 三 角 形 , ∠BAC=90°, AB=AC, BE 平 分 ∠ABC, CE⊥BE.求 证 :CE=1/2BD. 思路: 1. 构造全等(角平分线添加辅助线) 2. 内角平分线形成的∠A0C= 思路:构造全等(角平分线添加辅助线) (1)向两边作垂线 (2)翻折(截取)构造全等 思路:构造全等(角平分线添加辅助线) (3)“角平分线+垂直”构造等腰三角形 二、中点型 由 中 点 应 产 生 以 下 联 想 : 1、 利 用 中 心 对 称 图 形 构 造 8 字 型 全 等 三 角 形 2 、想 到 中 线 ,...